广东省汕头市潮阳区2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-08-04 类型:期末考试
一、选择题
-
1. 若式子 有意义,则x的取值范围为( )A、x≥2 B、x≠3 C、x≥2或x≠3 D、x≥2且x≠32. 下列各组数中,以a、b、c为边的三角形不是直角三角形的是( )A、a= ,b= ,c= B、a=1.5,b=2,c=3 C、a=6,b=8,c=10 D、a=3,b=4,c=53. 下列计算错误的是( )A、3+2 =5 B、÷2= C、× = D、- =4. 设n为正整数,且n<<n+1,则n的值为( )A、5 B、6 C、7 D、85. 若一个等腰直角三角形的面积为8,则这个等腰三角形的直角边长为( )A、2 B、4 C、4 D、86. 如图1,在平行四边形ABCD中,∠B=80°,AE平分∠BAD交BC于点E,CF∥AE交AD于点F,则∠1=( )
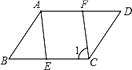 A、40° B、50° C、60° D、80°7. 小刚与小华本学期都参加5次数学考试(总分都为120分),数学老师想判断这两个同学的数学成绩谁更稳定,在做统计分析时,老师需要比较这两个人5次数学成绩的( )A、方差 B、平均数 C、众数 D、中位数8.
A、40° B、50° C、60° D、80°7. 小刚与小华本学期都参加5次数学考试(总分都为120分),数学老师想判断这两个同学的数学成绩谁更稳定,在做统计分析时,老师需要比较这两个人5次数学成绩的( )A、方差 B、平均数 C、众数 D、中位数8.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
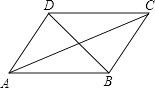 A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠DAB=90°时,四边形ABCD是正方形9. 关于一次函数y=﹣2x+3,下列结论正确的是( )A、图象过点(1,﹣1) B、图象经过一、二、三象限 C、y随x的增大而增大 D、当x> 时,y<010. 如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )
A、当AC=BD时,四边形ABCD是矩形 B、当AB=BC时,四边形ABCD是菱形 C、当AC⊥BD时,四边形ABCD是菱形 D、当∠DAB=90°时,四边形ABCD是正方形9. 关于一次函数y=﹣2x+3,下列结论正确的是( )A、图象过点(1,﹣1) B、图象经过一、二、三象限 C、y随x的增大而增大 D、当x> 时,y<010. 如图,菱形ABCD中,AB=2,∠B=120°,点M是AD的中点,点P由点A出发,沿A→B→C→D作匀速运动,到达点D停止,则△APM的面积y与点P经过的路程x之间的函数关系的图象大致是( )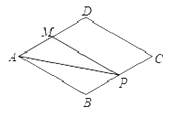 A、
A、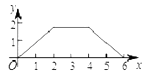 B、
B、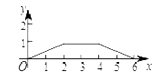 C、
C、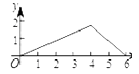 D、
D、
二、填空题
-
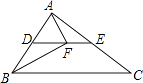
11. 比较大小:﹣2 ﹣3(填“<”或“=”或“>”)12. 将正比例函数y=﹣2x的图象沿y轴向上平移5个单位,则平移后所得图象的解析式是 .13. 在平面直角坐标系中,A(﹣4,3),点O为坐标原点,则线段OA的长为 .14. 如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为 .
 15. 如图,在△ABC中,∠ACB=90°,AC=6,AB=10,AB的垂直平分线DE交AB于点D,交BC于点E,则CE的长等于 .
15. 如图,在△ABC中,∠ACB=90°,AC=6,AB=10,AB的垂直平分线DE交AB于点D,交BC于点E,则CE的长等于 .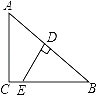 16. 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , …,照此规律作下去,则点B6的坐标为 .
16. 如图,在平面直角坐标系中有一个边长为1的正方形OABC,边OA,OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , …,照此规律作下去,则点B6的坐标为 .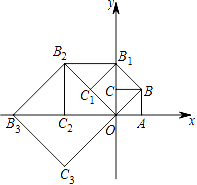
三、解答题
-
17. 计算: + ( ﹣1)﹣30﹣| ﹣2|.18. 先化简,再求值:(1﹣ )• ,其中a= ﹣1.19.
如图,在平行四边形ABCD中,已知AD>AB.
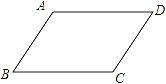 (1)、实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法).(2)、猜想并证明:猜想四边形ABEF的形状,并给予证明.20. 已知:x=2+ ,y=2﹣ .(1)、求代数式:x2+3xy+y2的值;(2)、若一个菱形的对角线的长分别是x和y,求这个菱形的面积?21. 甲、乙两校参加市教育局举办的初中生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
(1)、实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法).(2)、猜想并证明:猜想四边形ABEF的形状,并给予证明.20. 已知:x=2+ ,y=2﹣ .(1)、求代数式:x2+3xy+y2的值;(2)、若一个菱形的对角线的长分别是x和y,求这个菱形的面积?21. 甲、乙两校参加市教育局举办的初中生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.甲校成绩统计表

乙校成绩扇形统计图 乙校成绩条形统计图
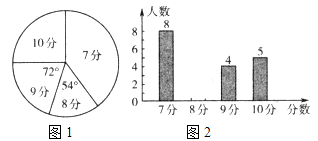 (1)、请将甲校成绩统计表和图2的统计图补充完整;(2)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.22. 已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)、请将甲校成绩统计表和图2的统计图补充完整;(2)、经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.22. 已知直线y=kx+5交x轴于A,交y轴于B且A坐标为(5,0),直线y=2x﹣4与x轴于D,与直线AB相交于点C.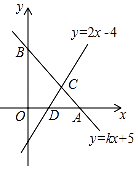 (1)、求点C的坐标;(2)、根据图象,写出关于x的不等式2x﹣4>kx+5的解集;(3)、求△ADC的面积.23. 某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费.小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.(1)、求每吨水的政府补贴优惠价和市场调节价分别是多少?(2)、设每月用水量为
(1)、求点C的坐标;(2)、根据图象,写出关于x的不等式2x﹣4>kx+5的解集;(3)、求△ADC的面积.23. 某地为了鼓励居民节约用水,决定实行两级收费制,即每月用水量不超过14吨(含14吨)时,每吨按政府补贴优惠价收费;每月超过14吨时,超过部分每吨按市场调节价收费.小英家1月份用水20吨,交水费29元;2月份用水18吨,交水费24元.(1)、求每吨水的政府补贴优惠价和市场调节价分别是多少?(2)、设每月用水量为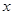 吨,应交水费为y元,写出y与
吨,应交水费为y元,写出y与 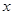 之间的函数关系式; (3)、小英家3月份用水24吨,她家应交水费多少元?24. 已知如图1,P为正方形ABCD的边BC上任意一点,BE⊥AP于点E,在AP的延长线上取点F,使EF=AE,连接BF,∠CBF的平分线交AF于点G.
之间的函数关系式; (3)、小英家3月份用水24吨,她家应交水费多少元?24. 已知如图1,P为正方形ABCD的边BC上任意一点,BE⊥AP于点E,在AP的延长线上取点F,使EF=AE,连接BF,∠CBF的平分线交AF于点G.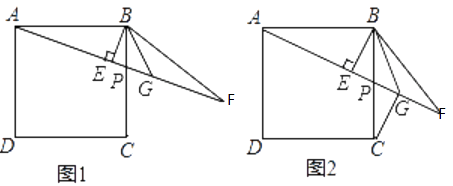 (1)、求证:BF=BC;(2)、求证:△BEG是等腰直角三角形;(3)、如图2,若正方形ABCD的边长为4,连接CG,当P点为BC的中点时,求CG的长.25. 如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(﹣4,4 ),点E是BC的中点,现将矩形折叠,折痕为EF,点F为折痕与y轴的交点,EF交x轴于G且使∠CEF=60°.
(1)、求证:BF=BC;(2)、求证:△BEG是等腰直角三角形;(3)、如图2,若正方形ABCD的边长为4,连接CG,当P点为BC的中点时,求CG的长.25. 如图,矩形OABC在平面直角坐标系内(O为坐标原点),点A在x轴上,点C在y轴上,点B的坐标为(﹣4,4 ),点E是BC的中点,现将矩形折叠,折痕为EF,点F为折痕与y轴的交点,EF交x轴于G且使∠CEF=60°.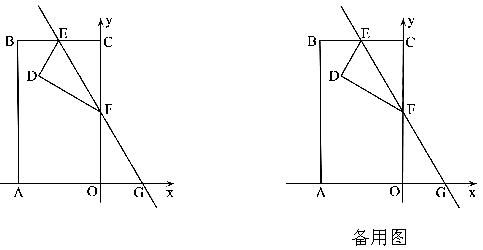 (1)、求证:△EFC≌△GFO;(2)、求点D的坐标;(3)、若点P(x,y)是线段EG上的一点,设△PAF的面积为s,求s与x的函数关系式并写出x的取值范围.
(1)、求证:△EFC≌△GFO;(2)、求点D的坐标;(3)、若点P(x,y)是线段EG上的一点,设△PAF的面积为s,求s与x的函数关系式并写出x的取值范围.