山东省东营市四校连赛（五四制）2016-2017学年八年级下学期期末考试数学试题

试卷更新日期：2017-08-04 类型：期末考试

进入出卷网下载

一、选择题

1. 若二次根式 $\sqrt{3 x - 2}$ 有意义，则x的取值范围是（）

A、x≥ $\frac{2}{3}$ B、x≤ $\frac{2}{3}$ C、x≥ $\frac{3}{2}$ D、x≤ $\frac{3}{2}$

查看试题解析
2. 已知点A（﹣2，y₁），B（3，y₂）在一次函数y=﹣x﹣2的图象上，则（　　）

A、y₁＞y₂ B、y₁＜y₂ C、y₁≤y₂ D、y₁≥y₂

查看试题解析
3. 若一个三角形的三边长分别为6、8、10，则这个三角形最长边上的中线长为（）

A、3.6 B、4 C、4.8 D、5

查看试题解析
4. 反比例函数 $y = \frac{6}{x}$ 与一次函数 $y = x + 1$ 的图象交于点 $A (2, 3)$ ，利用图象的对称性可知它们的另一个交点是（）.

A、 $(3, 2)$ B、 $(- 3, - 2)$ C、 $(- 2. - 3)$ D、 $(- 2, 3)$

查看试题解析
5. 某班学生积极参加爱心活动，该班50名学生的捐款统计情况如下表：
金额/元
5
10
20
50
100
人数
4
16
15
9
6
则他们捐款金额的中位数和平均数分别是（）

A、10，20.6 B、20，20.6 C、10，30.6 D、20，30.6

查看试题解析
6.
如图，在平面直角坐标系 $x O y$ 中，已知点 $A (\sqrt{2} ， 0)$ ， $B (1 ， 1)$ ．若平移点 $A$ 到点 $C$ ，使以点 $O$ ， $A$ ， $C$ ， $B$ 为顶点的四边形是菱形，则正确的平移方法是（）

A、向左平移1个单位，再向下平移1个单位 B、向左平移 $(2 \sqrt{2} - 1)$ 个单位，再向上平移1个单位 C、向右平移 $\sqrt{2}$ 个单位，再向上平移1个单位 D、向右平移1个单位，再向上平移1个单位

查看试题解析
7.
如图，在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB′E，AB′与CD边交于点F，则B′F的长度为（）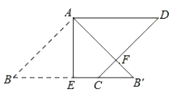

A、1 B、 $\sqrt{2}$ C、2- $\sqrt{2}$ D、2 $\sqrt{2}$ ﹣2

查看试题解析
8.
一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′，如图所示，∠DA′D′=45°，边BC与D′C′交于点O，则四边形ABOD′的周长是（）

A、6 B、6 $\sqrt{2}$ C、4 $\sqrt{2}$ D、3+3 $\sqrt{2}$

查看试题解析
9.
如图，在平行四边形ABCD中，对角线AC，BD相交于点 O，若BD，AC的和为18 cm， $CD ∶ DA = 2 ∶ 3$ ，△AOB的周长为13 cm，那么BC的长是（）

A、6 cm B、9 cm C、3 cm D、12 cm

查看试题解析

二、填空题

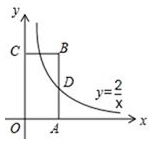
10. 直角三角形两直角边长分别为3和4，则它斜边上的高为．

查看试题解析
11. 已知一组数据为1，2，3，4，5，则这组数据的方差为．

查看试题解析
12. 已知一元二次方程x²+mx+m﹣1=0有两个相等的实数根，则m= ．

查看试题解析
13.
如图，反比例函数 $y = \frac{2}{x}$ 的图象经过矩形OABC的边AB的中点D，则矩形OABC的面积为.

查看试题解析
14.
如图，直线y＝x＋b与直线y＝kx＋6交于点P（3，5），则关于x的不等式x＋b＞kx＋6的解集是．

查看试题解析
15.
在矩形ABCD中，∠B的角平分线BE与AD交于点E，∠BED的角平分线EF与DC交于点F，若AB=9，DF=2FC，则BC= ．（结果保留根号）

查看试题解析
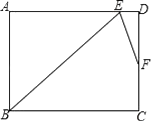16.
在平面直角坐标系中，直线l：y=x﹣1与x轴交于点A₁ ，如图所示依次作正方形A₁B₁C₁O、正方形A₂B₂C₂C₁、…、正方形A_nB_nC_nC_n_﹣1 ，使得点A₁、A₂、A₃、…在直线l上，点C₁、C₂、C₃、…在y轴正半轴上，则点B_n的坐标是．

查看试题解析

三、解答题。

17. 综合题

(1)、计算： $2 \sqrt{\frac{1}{3}} \times \sqrt{9} - \sqrt{12} + \sqrt[3]{\frac{7}{8} - 1}$ ．

(2)、用配方法解方程： $x^{2} - 10 x + 9 = 0$ .

查看试题解析
18.
如图，过点A（2，0）的两条直线l₁ ， l₂分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB= $\sqrt{13}$ ．

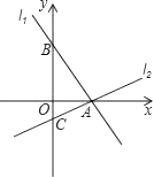(1)、求点B的坐标；

(2)、若△ABC的面积为4，求直线l₂的解析式．

查看试题解析
19.
垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩．测试规则为连续接球10个，每垫球到位1个记1分．
运动员甲测试成绩表
测试序号
1
2
3
4
5
6
7
8
9
10
成绩（分）
7
6
8
7
7
5
8
7
8
7

(1)、写出运动员甲测试成绩的众数和中位数；

(2)、在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适?为什么? (参考数据：三人成绩的方差分别为 $S_{甲}^{2} = 0.8$ 、 $S_{乙}^{2} = 0.4$ 、 $S_{丙}^{2} = 0.8$ )

查看试题解析
20.
已知：如图，在菱形ABCD 中，点E，O，F 分别是边AB，AC，AD的中点，连接CE、CF、OF．

(1)、求证：△ BCE≌△DCF；

(2)、当AB与BC满足什么条件时，四边形AEOF正方形？请说明理由．

查看试题解析
21. 某旅游景点为了吸引游客，推出的团体票收费标准如下：如果团体人数不超过25人，每张票价150元，如果超过25人，每增加1人，每张票价降低2元，但每张票价不得低于100元，阳光旅行社共支付团体票价4800元，则阳光旅行社共购买多少张团体票．

查看试题解析
22.
在直角墙角AOB（OA⊥OB，且OA、OB长度不限）中，要砌20m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96m² ．

(1)、求这地面矩形的长；

(2)、有规格为0.80×0.80和1.00×1.00（单位：m）的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面（不计缝隙），用哪一种规格的地板砖费用较少？

查看试题解析
23.
如图，已知反比例函数y= $\frac{k}{x}$ （k＜0）的图象经过点A（- $\sqrt{3}$ ，2），过点A作AB⊥x轴于点B，连结AO．

(1)、求k的值；

(2)、如图，若直线y=ax+b经过点A，与x轴相交于点C，且满足S_△ABC=2S_△AOC ．求：
①直线y=ax+b的表达式；
②记直线y=ax+b与双曲线y= $\frac{k}{x}$ （k＜0）的另一交点为D（n，﹣1），试求△AOD的面积S_△AOD以及使得不等式ax+b＞ $\frac{k}{x}$ 成立的x的取值范围．

查看试题解析
24.
如图1，在矩形纸片ABCD中，AB=3cm，AD=5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ.过点E作EF//AB交PQ于F，连接BF，

(1)、求证：四边形BFEP为菱形；

(2)、当E在AD边上移动时，折痕的端点P，Q也随着移动.
①当点Q与点C重合时，（如图2），求菱形BFEP的边长；
②如限定P，Q分别在BA，BC上移动，求出点E在边AD上移动的最大距离.

查看试题解析

金额/元	5	10	20	50	100
人数	4	16	15	9	6

测试序号	1	2	3	4	5	6	7	8	9	10
成绩（分）	7	6	8	7	7	5	8	7	8	7