河北省新乐市2018-2019学年九年级下学期数学开学考试试卷
试卷更新日期:2020-01-13 类型:开学考试
一、单选题
-
1. 如果∠A是锐角,且sinA= ,那么∠A的度数是( )A、90° B、60° C、45° D、30°2. 方程x2=4x的根是( )A、x=4 B、x=0 C、x1=0,x2=4 D、x1=0,x2=﹣43. 如图,在△ABC中,DE∥BC , 若 ,AE=1,则EC等于( )
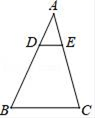 A、1 B、2 C、3 D、44. 如图所示,若△ABC∽△DEF,则∠E的度数为( )
A、1 B、2 C、3 D、44. 如图所示,若△ABC∽△DEF,则∠E的度数为( )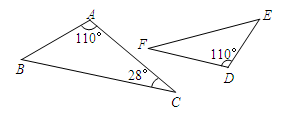 A、28° B、32° C、42° D、52°5. 下列一元二次方程中,有两个相等的实数根的是( )A、x2﹣4x﹣4=0 B、x2﹣36x+36=0 C、4x2+4x+1=0 D、x2﹣2x﹣1=06. 函数y= x2+1与y= x2图象不同之处是( )A、对称轴 B、开口方向 C、顶点 D、形状7. 点M(a,2a)在反比例函数y= 的图象上,那么a的值是( )A、4 B、﹣4 C、2 D、±28. 某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分.面试成绩为85分,那么吴老师的总成绩为( )分.A、85 B、86 C、87 D、889. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°10. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F , 那么△DEF的周长与△BAF的周长之比为( )
A、28° B、32° C、42° D、52°5. 下列一元二次方程中,有两个相等的实数根的是( )A、x2﹣4x﹣4=0 B、x2﹣36x+36=0 C、4x2+4x+1=0 D、x2﹣2x﹣1=06. 函数y= x2+1与y= x2图象不同之处是( )A、对称轴 B、开口方向 C、顶点 D、形状7. 点M(a,2a)在反比例函数y= 的图象上,那么a的值是( )A、4 B、﹣4 C、2 D、±28. 某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分.面试成绩为85分,那么吴老师的总成绩为( )分.A、85 B、86 C、87 D、889. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°10. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F , 那么△DEF的周长与△BAF的周长之比为( )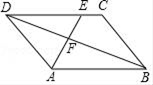 A、3:4 B、9:16 C、1:3 D、3:211. 如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠BCD等于( )
A、3:4 B、9:16 C、1:3 D、3:211. 如图,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠BCD等于( ) A、65° B、115° C、120° D、125°12. 郑州某中学在备考2018河南中考体育的过程中抽取该校九年级20名男生进 行立定跳远测试,以便知道下一阶段的体育训练,成绩如下所示:
A、65° B、115° C、120° D、125°12. 郑州某中学在备考2018河南中考体育的过程中抽取该校九年级20名男生进 行立定跳远测试,以便知道下一阶段的体育训练,成绩如下所示:
则下列叙述正确的是( )
A、这些运动员成绩的众数是5 B、这些运动员成绩的中位数是2.30 C、这些运动员的平均成绩是2.25 D、这些运动员成绩的方差是0.072 513. 如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD . 若∠ACD=48°,则∠DBA的大小是( )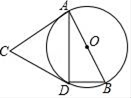 A、32° B、48° C、60° D、66°14. 如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
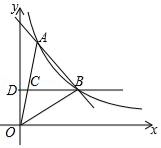
A、32° B、48° C、60° D、66°14. 如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )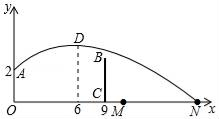 A、球不会过网 B、球会过球网但不会出界 C、球会过球网并会出界 D、无法确定15. 如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y= 的图象经过点D , 则k值为( )
A、球不会过网 B、球会过球网但不会出界 C、球会过球网并会出界 D、无法确定15. 如图,平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y= 的图象经过点D , 则k值为( ) A、﹣14 B、14 C、7 D、﹣716. 如图,点M为▱ABCD的边AB上一动点,过点M作直线l垂直于AB,且直线l与▱ABCD的另一边交于点N.当点M从A→B匀速运动时,设点M的运动时间为t,△AMN的面积为S,能大致反映S与t函数关系的图象是( )
A、﹣14 B、14 C、7 D、﹣716. 如图,点M为▱ABCD的边AB上一动点,过点M作直线l垂直于AB,且直线l与▱ABCD的另一边交于点N.当点M从A→B匀速运动时,设点M的运动时间为t,△AMN的面积为S,能大致反映S与t函数关系的图象是( )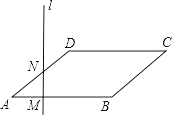 A、
A、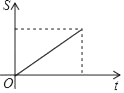 B、
B、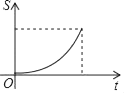 C、
C、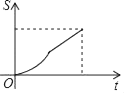 D、
D、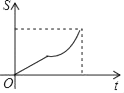
二、填空题
-
17. 已知反比例函数y= 图象位于一、三象限,则m的取值范围是 .18. 如图,四边形 ABCD 内接于⊙O ,AB 为⊙O 的直径,点 C 为弧 BD 的中点.若∠DAB=40°,则∠ABC= .
 19. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为 .
19. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为 .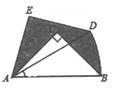
三、解答题
-
20. 规定:身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级500名男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理统计表:

根据以上表格信息,解答如下问题:
(1)、计算这组数据的三个统计量:平均数、中位数、众数;(2)、请你选择其中一个统计量作为选定标准,估计该校九年级男生中具有“普通身高”的人数.21. 某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:

②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
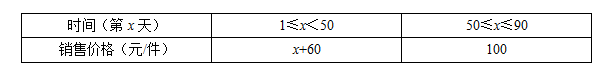 (1)、求出第10天日销售量;(2)、设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格﹣每件成本))(3)、在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.22. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED , DF:DC=1:4,连接EF并延长交BC的延长线于点G .
(1)、求出第10天日销售量;(2)、设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格﹣每件成本))(3)、在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.22. 如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED , DF:DC=1:4,连接EF并延长交BC的延长线于点G .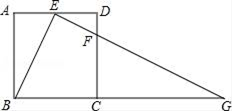 (1)、求证:△ABE∽△DEF;(2)、若正方形的边长为10,求BG的长.23. 如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号)
(1)、求证:△ABE∽△DEF;(2)、若正方形的边长为10,求BG的长.23. 如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上).已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果保留根号) 24. 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
24. 如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P. (1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.
(1)、求证:PD是⊙O的切线;(2)、求证:△PBD∽△DCA;(3)、当AB=6,AC=8时,求线段PB的长.