山东省泰安市新泰市西部联盟2019-2020学年九年级上学期数学第二次联考试题

试卷更新日期：2020-01-13 类型：月考试卷

进入出卷网下载

一、选择题（本大题共12小题，共48分）

1. 在Rt△ABC中，cosA= $\frac{1}{2}$ ，那么sinA的值是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{1}{2}$

查看试题解析
2. a、b是实数，点 A（2，a）、 B（3，b）在反比例函数 $y =- \frac{2}{x}$ 的图象上，则（）

A、 $a < b < 0$ B、 $b < a < 0$ C、 $a < 0 < b$ D、 $b < 0 < a$

查看试题解析
3. 将抛物线y=-3x²平移，得到抛物线y=-3（x-1）²-2，下列平移方式中，正确的是（）

A、先向左平移1个单位，再向上平移2个单位 B、先向左平移1个单位，再向下平移2个单位 C、先向右平移1个单位，再向上平移2个单位 D、先向右平移1个单位，再向下平移2个单位

查看试题解析
4. 如图，直线l⊥x轴于点P ，且与反比例函数 $y_{1}$ = $\frac{k_{1}}{x}$ （x＞0）及 $y_{2}$ = $\frac{k_{2}}{x}$ （x＞0）的图象分别交于点A ， B ，连接OA ， OB ，已知△OAB的面积为2，则k₁-k₂的值为（）

A、2 B、3 C、4 D、 $- 4$

查看试题解析
5. 如图，在矩形ABCD中，AB=3，AD=5，点E在DC上，将矩形ABCD沿AE折叠，点D恰好落在BC边上的点F处，那么cos∠EFC的值是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
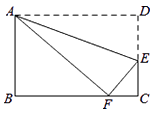6. 已知函数y=（k-1）x²-4x+4与x轴只有一个交点，则k的取值范围是（）

A、 $k \leq 2$ 且 $k \neq 1$ B、 $k < 2$ 且 $k \neq 1$ C、 $k = 2$ D、 $k = 2$ 或1

查看试题解析
7. 如图，AB是⊙O的一条弦，OD⊥AB于点C，交⊙O于点D，连接OA．若AB=4，CD=1，则⊙O的半径为（）

A、5 B、 $\sqrt{5}$ C、3 D、 $\frac{5}{2}$

查看试题解析
8. 如图，等腰直角△ABC中，AB＝AC＝8，以AB为直径的半圆O交斜边BC于D ，则阴影部分面积为（结果保留π）（）

A、16 B、 $24 - 4 π$ C、 $32 - 4 π$ D、 $32 - 8 π$

查看试题解析
9. 反比例函数 $y = \frac{k^{2} + 1}{x}$ 图象上有三个点（x₁ ， y₁），（x₂ ， y₂），（x₃ ， y₃），其中x₁＜x₂＜0＜x₃ ，则y₁ ， y₂ ， y₃的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
10. 如图所示，为了测得电视塔的高度AB ，在D处用高为1米的测角仪CD ，测得电视塔顶端A的仰角为30°，再向电视塔方向前进120米达到F处，又测得电视塔顶端A的仰角为60°，则这个电视塔的高度AB（单位：米）为（）

A、 $60 \sqrt{3}$ B、61 C、 $60 \sqrt{3} + 1$ D、121

查看试题解析
11. 在同一平面直角坐标系中，函数y=ax+b与y=ax²-bx的图象可能是（）

A、 B、 C、 D、

查看试题解析
12. 抛物线 $y = a x^{2} + b x + c$ 的顶点为 $D (- 1 ， 2)$ ，与x轴的一个交点A在点 $(- 3 ， 0)$ 和 $(- 2 ， 0)$ 之间，其部分图象如图，则以下结论： $① b^{2} - 4 a c < 0$ ； $②$ 当 $x > - 1$ 时，y随x增大而减小； $③ a + b + c < 0$ ； $④$ 若方程 $a x^{2} + b x + c - m = 0$ 没有实数根，则 $m > 2$ ； $⑤ 3 a + c < 0.$ 其中符合题意结论的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题（本大题共6小题，共24分）

13. 如图，在平面直角坐标系中，Rt△ABO的顶点O与原点重合，顶点B在x轴上，∠ABO=90°，OA与反比例函数y= $\frac{k}{x}$ 的图象交于点D ，且OD=2AD ，过点D作x轴的垂线交x轴于点C ．若S_四边形_ABCD=10，则k的值为．

查看试题解析
14. 当-1≤x≤1时，二次函数y=-（x-m）²+m²+1有最大值4，则实数m的值为．

查看试题解析
15. 如图，已知⊙O是△ABC的内切圆，切点为D、E、F ，如果AE=2，CD=1，BF=3，则内切圆的半径r= ．

查看试题解析
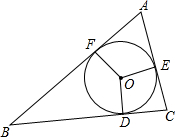16. 在某一时刻，测得一根高为2m的竹竿的影长为1m ，同时测得一栋建筑物的影长为9m ，那么这栋建筑物的高度为m ．

查看试题解析
17. 如图，直线l⊥x轴于点P ，且与反比例函数y₁= $\frac{k_{1}}{x}$ （x＞0）及y₂= $\frac{k_{2}}{x}$ （x＞0）的图象分别交于点A ， B ，连接OA ， OB ，已知△OAB的面积为3，则k₁-k₂= ．

查看试题解析

三、解答题（本大题共8小题，共78分）

18. 计算：

(1)、4cos30°+（1- $\sqrt{2}$ ）⁰- $\sqrt{12}$ +|-2|．

(2)、计算：|-2|×cos60°-（ $\frac{1}{3}$ ）^-1 ．

查看试题解析
19. 如图，直线y=-x+b与反比例函数 $y = - \frac{3}{x}$ 的图象相交于点A（a ， 3），且与x轴相交于点B ．

(1)、求a、b的值；

(2)、若点P在x轴上，且△AOP的面积是△AOB的面积的 $\frac{1}{2}$ ，求点P的坐标．

查看试题解析
20.
如图，在大楼AB正前方有一斜坡CD，坡角∠DCE=30°，楼高AB=60米，在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的D处测得楼顶B的仰角为45°，其中点A，C，E在同一直线上.

(1)、求坡底C点到大楼距离AC的值；

(2)、求斜坡CD的长度.

查看试题解析
21. 如图，反比例函数 $y_{1} = \frac{m}{x}$ 的图象与一次函数y₂=kx+b的图象交于A、B两点．已知A（2，n），B（- $\frac{1}{2}$ ，-2）．

(1)、求反比例函数和一次函数的解析式；

(2)、求△AOB的面积；

(3)、请结合图象直接写出当y₁≥y₂时自变量x的取值范围．

查看试题解析
22. 如图，AB是⊙O的直径，点C在AB的延长线上，AD平分∠CAE交⊙O于点D ，且AE⊥CD ，垂足为点E ．

(1)、求证：直线CE是⊙O的切线．

(2)、若BC=3，CD=3 $\sqrt{2}$ ，求弦AD的长．

查看试题解析
23. 某超市准备进一批每个进价为40元的小家电，经市场调查预测，售价定为50元时可售出400个；定价每增加1元，销售量将减少10个．

(1)、设每个定价增加x元，此时的销售量是多少？（用含x的代数式表示）

(2)、超市若准备获得利润6000元，并且使进货量较少，则每个应定价为多少元？

(3)、超市若要获得最大利润，则每个应定价多少元？获得的最大利润是多少？

查看试题解析
24. 已知，如图，抛物线y=-x²+bx+c经过直线y=-x+3与坐标轴的两个交点A ， B ，此抛物线与x轴的另一个交点为C ，抛物线的顶点为D ．

(1)、求此抛物线的解析式；

(2)、若点M为抛物线上一动点，是否存在点M ，使△ACM与△ABC的面积相等？若存在，求点M的坐标；若不存在，请说明理由．

(3)、在x轴上是否存在点N使△ADN为直角三角形？若存在，确定点N的坐标；若不存在，请说明理由．

查看试题解析