广东省佛山市顺德区2019-2020学年八年级上学期数学第15周教研联盟测试

试卷更新日期：2020-01-13 类型：月考试卷

进入出卷网下载

一、选择题(本大题共10小题，每小题3分，共30分)

1. 下列各组数，可以作为直角三角形的三边长的是（）

A、8，12，20 B、2，3，4 C、5，12，13 D、4，5，6

查看试题解析
2. 下列各数中，为无理数的是（）

A、 $\sqrt[3]{27}$ B、 $\sqrt{4}$ C、3.1415926 D、 $\sqrt{2}$

查看试题解析
3. 下列计算中，正确的是（）

A、 $\sqrt{4}$ ＝±2 B、 $\sqrt{3}$ + $\sqrt{2}$ ＝ $\sqrt{5}$ C、 $\sqrt{9}$ + $\sqrt{3}$ ＝3 D、 $\sqrt[3]{- 8}$ ＝ $- 2$

查看试题解析
4. 下列坐标点在第四象限内的是（）

A、（1，2） B、（﹣1，﹣2） C、（﹣1，2） D、（1，﹣2）

查看试题解析
5. 下面是二元一次方程2x﹣y＝1的解的是（）

A、 ${\begin{matrix} x = 4 \\ y = 7 \end{matrix}$ B、 ${\begin{matrix} x = 0 \\ y = - 0.5 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = - 1 \end{matrix}$ D、 ${\begin{matrix} x = 5 \\ y = - 3 \end{matrix}$

查看试题解析
6. 小红连续6次掷骰子得到的点数分别是5、4、4、2、1、6．则这组数据的众数是（）

A、5 B、4 C、2 D、6

查看试题解析
7. 已知点P的坐标为（4，7），则点P到x轴的距离是（）

A、4 B、5 C、7 D、11

查看试题解析
8. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，以点A为圆心，AC长为半径画弧，交AB于点D ，则BD的值是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 直线y＝﹣x+3经过的象限是（）

A、第一、二、四象限 B、第一、二、三象限 C、第二、三、四象限 D、第一、三、四象限

查看试题解析
10. 如图，直线l：y＝x+1交y轴于点A₁ ，在x轴正方向上取点B₁ ，使OB₁＝OA₁；过点B₁作A₂B₁⊥x轴，交l于点A₂ ，在x轴正方向上取点B₂ ，使B₁B₂＝B₁A₂；过点B₂作A₃B₂⊥x轴，交l于点A₃ ，在x轴正方向上取点B₃ ，使B₂B₃＝B₂A₃；…记△OA₁B₁面积为S₁ ， △B₁A₂B₂面积为S₂ ， △B₂A₃B₃面积为S₃ ， …则S₂₀₁₇等于（）

A、2⁴⁰³⁰ B、2⁴⁰³¹ C、2⁴⁰³² D、2⁴⁰³³

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分）

11. 某射击运动员在一次射击训练中，共射击了6次，所得成绩（单位：环）为：6、8、7、7、8、9，这组数据的中位数为。

查看试题解析
12. 直线y=7x向上平移2个单位得到直线的关系式是。

查看试题解析
13. 点M（﹣1，y₁），N（3，y₂）在该函数y=﹣ $\frac{1}{2}$ x+1的图象上，则y₁ y₂（填>、< 或=）．

查看试题解析
14. 设n为正整数，且n< $\sqrt{65}$ <n+1，则n的值是。

查看试题解析
15. 如图，已知函数 y=ax+b 和 y=kx 的图象交于点P，则根据图象可得，关于 $\{\begin{cases} y = a x + b \\ y = k x \end{cases}$ 的二元一次方程组的解是。

查看试题解析
16. $\sqrt[3]{27}$ 16.如图1是由四个全等的直角三角形围成．若较短的直角边BC=5，将四个直角三角形中较长的直角边分别向外延长一倍，得到图2所示的“数学风车”，若△BCD的周长是30，则这个风车的外围周长是．

查看试题解析

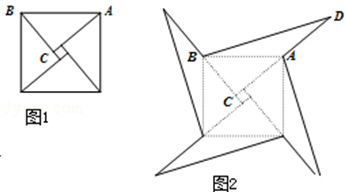
三、解答题（一）（每小题6分，共18分）

17. 计算： $\sqrt{6} \times \sqrt{3} - 6 \sqrt{\frac{1}{2}} + \sqrt{8}$

查看试题解析
18. 如图

(1)、画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出B₁的坐标；

(2)、求出△ABC的面积。

查看试题解析
19. 今年5月10日母亲节那天，某班很多同学给妈妈准备了鲜花和礼盒，根据图中的信息求每束鲜花和一个礼盒的价格。

查看试题解析

四、解答题（二）（每小题7分，共21分）

20. 如图，已知在△ABC中，AB＝AC＝13cm，D是AB上一点，且CD＝12cm，BD＝8cm．

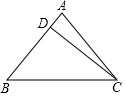(1)、求证：△ADC是直角三角形；

(2)、求BC的长

查看试题解析
21. A、B两店分别选5名销售员某月的销售额（单位：万元）进行分析，数据如下图表（不完整）：

平均数

中位数

众数

A店

8.5





B店



8

10

(1)、根据图a数据填充表格b所缺的数据；

(2)、如果A店想让一半以上的销售员达到销售目标，你认为月销售额定为多少合适？说明理由．

查看试题解析
22. 已知一次函数y＝2x﹣4

(1)、在平面直角坐标系中画出图象；

(2)、该直线与x轴相交于点A，与y轴相交于点B，线段AB上有点C( 1，-2)，在y轴上有一动点P，请求出PA+PC的最小值。

查看试题解析

五、解答题（三）（每小题9分，共27分）

23. 张庄甲、乙两家草莓采摘园的草莓销售价格相同，“春节期间”，两家采摘园将推出优惠方案，甲园的优惠方案是：游客进园需购买门票，采摘的草莓六折优惠；乙园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，某游客的草莓采摘量为x（千克），在甲园所需总费用为y_甲（元），在乙园所需总费用为y_乙（元），y_甲、y_乙与x之间的函数关系如图所示，折线OAB表示y_乙与x之间的函数关系．

(1)、甲采摘园的门票是元，两个采摘园优惠前的草莓单价是每千克元；

(2)、当x＞10时，求y_乙与x之间的函数关系式；

(3)、游客在“春节期间”采摘多少千克草莓时，甲、乙两家采摘园的总费用相同．

查看试题解析
24. 观察下列一组等式的化简，然后解答后面的问题：
$\frac{1}{\sqrt{2} + 1}$ ＝ $\frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)}$ ＝ $\sqrt{2}$ ﹣1；

$\frac{1}{\sqrt{3} + \sqrt{2}}$ ＝ $\frac{1 \times (\sqrt{3} - \sqrt{2})}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})}$ ＝ $\sqrt{3}$ ﹣ $\sqrt{2}$ ；

$\frac{1}{\sqrt{4} + \sqrt{3}}$ ＝ $\frac{1 \times (\sqrt{4} - \sqrt{3})}{(\sqrt{4} + \sqrt{3}) (\sqrt{4} - \sqrt{3})}$ ＝ $\sqrt{4}$ ﹣ $\sqrt{3}$ ＝2﹣ $\sqrt{3}$ ；

(1)、从上述化简中找出规律 $\frac{1}{\sqrt{n + 1} + \sqrt{n}}$ ＝（n为正整数）；

(2)、比较 $\sqrt{2019}$ ﹣ $\sqrt{2018}$ 与 $\sqrt{2018}$ ﹣ $\sqrt{2017}$ 的大小；

(3)、利用你发现的规律计算下列式子的值：
（ $\frac{1}{\sqrt{2} + 1}$ + $\frac{1}{\sqrt{3} + \sqrt{2}}$ + $\frac{1}{\sqrt{4} + \sqrt{3}}$ +…+ $\frac{1}{\sqrt{2019} + \sqrt{2018}}$ ）（ $\sqrt{2019}$ +1）

查看试题解析
25. 如图，在平面直角坐标系xOy中，直线y＝﹣ $\frac{1}{2}$ x+ $\frac{3}{2}$ 与y＝x相交于点A ，与x轴交于点B ．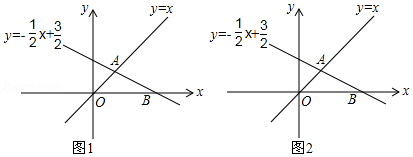

(1)、填空：A的坐标是， B的坐标是；

(2)、直线y＝﹣ $\frac{1}{2}$ x+ $\frac{3}{2}$ 上有点P(m，n)，且点P在第四象限，设△AOP的面积为S，
请求出S与m的函数关系式；

(3)、在直线OA上，是否存在一点D ，使得△DOB是等腰三角形？如果存在，试求出所有符合条件的点D的坐标，如果不存在，请说明理由。

查看试题解析

	平均数	中位数	众数
A店	8.5
B店		8	10