江苏省兴化市顾庄学区三校2016-2017学年八年级下学期期末考试数学试题

试卷更新日期：2017-08-04 类型：期末考试

进入出卷网下载

一、选择题

1. 二次根式 $\sqrt{2 - x}$ 有意义，则 $x$ 的取值范围是（）

A、 $x > 2$ B、 $x < 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
2. 分式 $- \frac{1}{1 - x}$ 可变形为（）

A、 $- \frac{1}{x - 1}$ B、 $- \frac{1}{1 + x}$ C、 $\frac{1}{1 + x}$ D、 $\frac{1}{x - 1}$

查看试题解析
3. 在平面直角坐标系xOy中，⊙O的半径为4，点P的坐标为（3，4），则点P的位置为（）

A、在⊙A外 B、在⊙A 上 C、在⊙A 内 D、不确定

查看试题解析
4. 对于反比例函数 $y = \frac{2}{x}$ ，下列说法不正确的是（）

A、点（-2，-1）在它的图像上 B、它的图像在第一、三象限 C、当 $x > 0$ 时，y随x的增大而增大 D、当 $x < 0$ 时，y随x的增大而减小

查看试题解析
5. 兴化市“菜花节”观赏人数逐年增加，据有关部门统计，2015年约为20万人次，2017年约为28.8万人次，设观赏人数年均增长率为x，则下列方程中正确的是（）

A、 $20 （ 1 + 2 x) = 28.8$ B、 $28.8 （ 1 + x)^{2} = 20$ C、 $20 （ 1 + x)^{2} = 28.8$ D、 $20 + 20 （ 1 + x) + 20 （ 1 + x)^{2} = 28.8$

查看试题解析
6. 有下列五个命题：①半圆是弧，弧是半圆；②周长相等的两个圆是等圆；③半径相等的两个半圆是等弧；④直径是圆的对称轴；⑤直径平分弦与弦所对的弧. 其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 当a ＝时，分式 $\frac{a + 3}{a - 2}$ 的值为－4．

查看试题解析
8. 分式 $\frac{y}{5 x^{2}}$ 和 $\frac{y}{2 x^{5}}$ 的最简公分母是．

查看试题解析
9. 比较大小： $1$ $\sqrt{3} - 1$ （填“﹤”，“＝”，“﹥”）.

查看试题解析
10. 以3、－5为根且二次项系数为1的一元二次方程是．

查看试题解析
11. 当1＜P＜2时，代数式 $\sqrt{{(1 - p)}^{2}} + {(\sqrt{2 - p})}^{2}$ 的值为．

查看试题解析
12. 已知y是x的反比例函数，且当x＝2时，y＝－3. 则当y＝2时，x = ．

查看试题解析
13. 关于x的一元二次方程 $(a - 2) x^{2} + x + a^{2} - 4 = 0$ 的一个根为0，则a的值为．

查看试题解析
14.
如图，已知⊙O的半径为5，点P是弦AB上的一动点，且弦AB的长为8．则OP的取值范围为．

查看试题解析
15. 用配方法求得代数式 $3 x^{2} + 6 x - 7$ 的最小值是．

查看试题解析
16. 若直角三角形的两边a、b是方程 $x^{2} - 7 x + 12 = 0$ 的两个根，则该直角三角形的内切圆的半径r = ．

查看试题解析
17. 计算：

(1)、 $\frac{1}{2} \sqrt{12} - (3 \sqrt{\frac{1}{3}} + \sqrt{5})$

(2)、 $2017^{0} + \sqrt{8} + 2 \times 2^{- 1} - | \sqrt{2} - 2 |$

查看试题解析
18. 解方程：

(1)、 $x + 3 - x (x + 3) = 0$ ；

(2)、 $\frac{x - 2}{x + 2} - \frac{x + 2}{x - 2} = \frac{16}{x^{2} - 4}$ ．

查看试题解析
19. 先化简，再求值： $\frac{a^{2} - b^{2}}{a} \div (a - \frac{2 a b - b^{2}}{a})$ ，其中 $a = 2 + \sqrt{3}$ ， $b = 2 - \sqrt{3}$ ．

查看试题解析
20. 小明用12元买软面笔记本，小丽用21元买硬面笔记本，已知每本硬面笔记本比软面笔记本贵1.2元，小明和小丽能买到相同数量的笔记本吗？

查看试题解析
21. 已知反比例函数 $y = \frac{1 - k}{x}$ 的图像经过点A（2，－4）.

(1)、求k的值；

(2)、它的图像在第象限内，在各象限内，y随x增大而；（填变化情况）

(3)、当－2 ≤ x ≤－ $\frac{1}{2}$ 时，求y的取值范围．

查看试题解析
22.
如图，已知BC是⊙O的直径，A是⊙O上一点，AD⊥BC，垂足为D， $\overset{}{弧A E}$ =弧AB，BE交AD于点F．

(1)、∠ACB与∠BAD相等吗？为什么？

(2)、判断△FAB的形状，并说明理由．

查看试题解析
23. 花鸟市场一家店铺正销售一批兰花,每盆进价100元,售价为140元,平均每天可售出20盆.为扩大销量,增加利润,该店决定适当降价.据调查,每盆兰花每降价1元,每天可多售出2盆. 要使得每天利润达到1200元，则每盆兰花售价应定为多少元？

查看试题解析
24. 关于x的二次方程 $（ k - 1) x^{2} + 2 k x + 2 = 0$ .

(1)、求证：无论k为何值，方程总有实数根.

(2)、设 $x_{1}$ 、 $x_{2}$ 是方程 $（ k - 1) x^{2} + 2 k x + 2 = 0$ 的两个根，记 $S = \frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}} + x_{1} + x_{2}$ ， $S$ 的值能为2吗？若能，求出此时k的值.若不能，请说明理由.

查看试题解析
25.
如图，在△ABC中，⊙O经过A、B两点，圆心O在BC边上，且⊙O与BC边交于点E，在BC上截取CF=AC，连接AF交⊙O 于点D，若点D恰好是 $\overset{}{弧B E}$ 的中点．

(1)、求证：AC是⊙O的切线；

(2)、若BF=17，DF=13，求⊙O的半径r；

(3)、若∠ABC=30°，动直线l从与点A、O重合的位置开始绕点O顺时针旋转，到与OC重合时停止，设直线l与AC的交点为F，点Q为OF的中点，过点F作FG⊥BC于G，连接AQ、QG．请问在旋转过程中，∠AQG的大小是否变化？若不变，求出∠AQG的度数；若变化，请说明理由．

查看试题解析
26.
如图1，正方形ABCD顶点A、B在函数y= $\frac{k}{x}$ （k﹥0）的图像上，点C、D分别在x轴、y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．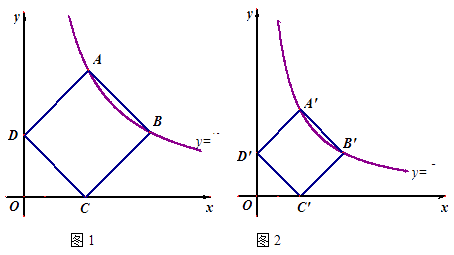

(1)、若点A的横坐标为3，求点D的纵坐标；

(2)、如图2，当k=8时，分别求出正方形A′B′C′D′的顶点A′、B′ 两点的坐标；

(3)、当变化的正方形ABCD与（2）中的正方形A′B′C′D′有重叠部分时，求k的取值范围．

查看试题解析