广东省中山市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期：2020-01-13 类型：期末考试
一、单项选择题(共10个小题，每小题3分，满分30分)
-
1. 下列四个手机APP图标中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知某细菌直径长约0.0000152米，那么该细菌的直径长用科学记数法表示为（ ）A、1.52×10-5米 B、1.52×105米 C、1.52×104米 D、1.52×10-4米3. 下列等式成立的是（ ）A、x2+x3=x5 B、(a-b)2=a2-b2 C、(x2)3=x6 D、(-1)0=-14. 点P(2，-1)关于y轴的对称点坐标是（ ）A、(2，1) B、(-1，2) C、(-2，1) D、(-2，-1)5. 若分式 ，则（ ）A、x≠0 B、x=2 C、x=0 D、x=0或x=26. 下列因式分解正确的是（ ）A、x2+y2=(x+y)2 B、x4-y4=(x2+y2)(x2-y2) C、-3a+12=-3(a-4) D、a2+7a-8=a(a+7)-87. 一边长为3，另一边长为6的等腰三角形的周长是（ ）A、12 B、15 C、12或15 D、98. 已知 ，则 的值为（ ）A、6 B、-6 C、 D、9. 如图，AD是△ABC的角平分线，DE⊥AB，AB=6cm，DE=4cm，S△ABC=30cm2 ， 则AC的长为（ ）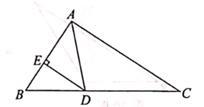
A、10cm B、9cm C、4.5cm D、3cm10. 如图，Rt△ACB中，∠ACB=90°，∠A=60°，CD，CE分别是△ABC的高和中线，下列说法错误的是（ ）
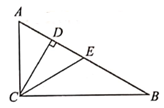A、AD=DE B、S△CEB=S△ACE C、AC，BC的垂直平分线都经过点E D、图中只有一个等腰三角形二、填空题(共7个小题，每小题4分，满分28分)
-
11. 计算：(-2a2)3÷a2=。12. 如图，在△ABC中，D是BC延长线上一点，∠A=68°，∠B=65°，则∠ACD= 。
13. 如图，BC=EF，AC∥DF。请你添加一个适当的条件，使得△ABC≌△DEF。（只需填一个答案即可)
14. 方程 的解x=。15. 已知ab=-3，a+b=5，则10+a2b+ab2=。16. 关于x的分式方程 的解为正数，则m的取值范围是 ．17. 如图，∠AOB=30°，点P是∠AOB内任意一点，且OP=7，点E和点F分别是射线OA和射线OB上的动点，则△PEF周长的最小值是 。
三、解答题(一)(共3个小题，每小题6分，满分18分)
-
18. 计算：(2x-1)2-x(4x-1)19. 先化简，再求值： ，其中a=-1。20. 如图，已知△ABC中，∠BAC=23°，∠BCA=125°。
(1)、尺规作图：作AC的垂直平分线，交BC的延长线于点D(不写作法，保留作图痕迹)；(2)、连接AD，求∠BAD的度数。四、解答题(二)(共3个小题，每小题8分，满分24分)
-
21. 如图，已知△ABC≌△DEF，BG、EH分别是△ABC和△DEF的中线．求证：BG=EH。
22. 如图，△ABC中，AE=BE，∠AED=∠ABC。
(1)、求证：BD平分∠ABC；(2)、若AB=CB，∠AED=4∠EAD，求∠C的度数。23. 某商家用1000元购进一批多肉盆栽，很快售完，接着又用了1600元购进第二批多肉盆栽，且数量是第一批的1.2倍，已知第一批盆栽的单价比第二批的单价少3元，问这两批多肉盆栽的单价各是多少元?五、解答题(三)(共2个小题，每小题10分，满分20分)
-
24. 如图，在△ABC中，∠ACB=90°，AC=BC，D为BC边的中点，BE⊥AB交AD的延长线于点E，CF平分∠ACB交AD于点F，连接CE。
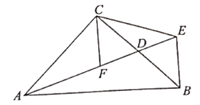
求证：
(1)、点D是EF的中点；(2)、△CEF是等腰三角形。25. 已知△ABC中，∠B=60°，点D是AB边上的动点，过点D作DE∥BC交AC于点E，将△ADE沿DE折叠，点A对应点为F点。(1)、如图(1)，当点F恰好落在BC边上，求证：△BDF是等边三角形；
(2)、如图(2)，当点F落在△ABC内，且DF的延长线恰好经过点C，CF=EF，求∠A的大小；
(3)、如图(3)，当点F落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB=9，求BG的长。
