江苏省昆山市、太仓市2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-08-04 类型:期末考试
一、选择题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下面调查中,适合采用普查的是( )A、调查你所在的班级同学的身高情况 B、调查全国中学生心理健康现状 C、调查我市食品合格情况 D、调查中央电视台《少儿节目》收视率3. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、4. 下列事件中,属于必然事件的是( )
2. 下面调查中,适合采用普查的是( )A、调查你所在的班级同学的身高情况 B、调查全国中学生心理健康现状 C、调查我市食品合格情况 D、调查中央电视台《少儿节目》收视率3. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、4. 下列事件中,属于必然事件的是( )
A、某校初二年级共有480人,则至少有两人的生日是同一天 B、经过路口,恰好遇到红灯 C、打开电视,正在播放动画片 D、抛一枚硬币,正面朝上5. 下列二次根式的运算:① ;② ;③ ;④ ;其中运算正确的有( )A、1个 B、2个 C、3个 D、4个6. 如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为( ) A、12 B、13 C、14 D、157. 若分式方程 有增根,则 的值是( )A、1 B、2 C、3 D、48. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A、12 B、13 C、14 D、157. 若分式方程 有增根,则 的值是( )A、1 B、2 C、3 D、48. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )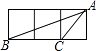 A、
A、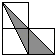 B、
B、 C、
C、 D、
D、 9. 函数 ( 为常数)的图像上游三个点 ,函数值 的大小为( )A、 B、 C、 D、10. 如图①,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为 ,△ABP的面积为 ,如果 关于 的函数图象如图 ②所示,则△ABC的面积是( )
9. 函数 ( 为常数)的图像上游三个点 ,函数值 的大小为( )A、 B、 C、 D、10. 如图①,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为 ,△ABP的面积为 ,如果 关于 的函数图象如图 ②所示,则△ABC的面积是( )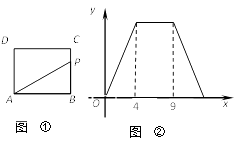 A、10 B、16 C、18 D、20
A、10 B、16 C、18 D、20二、填空题
-
11. 若最简二次根式 是同类二次根式,则a的值为;12. 一只不透明的袋子中有1个白球、1个红球和2个黄球,这些球除颜色不同外其它都相同.搅均后从中任意摸出1个球,摸出白球可能性 摸出黄球可能性.(填“等于”或“小于”或“大于”).13. 某一时刻,身高1. 6m的小明在阳光下的影长是0.4m,同一时刻同一地点测得旗杆的影长是3m,则该旗杆的高度是 m.14. 矩形的两条对角线的夹角为60°,较短的边长为12cm,则矩形较长的边长m.15. 如图, 中,点E、F为对角线BD上两点,请添加一个条件,使四边形AECF成为平行四边形:.
 16. 曲线 与直线 相交于点P ,则 =.17. 如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的有()
16. 曲线 与直线 相交于点P ,则 =.17. 如图,将一个等腰直角三角形按图示方式依次翻折,若DE=a,则下列说法正确的有()①DC′平分∠BDE;②BC长为 ;③△ 是等腰三角形;④△CED的周长等于BC的长.

A.1个 B.2个 C.3个 D.4个
三、解答题
-
18. 计算:19. 解方程:20. 先化简 ,然后从不等组 的解集中,选取一个你认为符合题意的x的值代入求值.21. 在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:


请你根据以上信息解答下列问题:
(1)、这次栽下的四个品种的树苗共棵,乙品种树苗棵;(2)、图1中,甲%、乙%,并将图2补充完整;(3)、若经观测计算得出丙种树苗的成活率为89.6%,求这次植树活动的树苗成活率.
22. 如图在平面直角坐标系xOy中,函数 ( )的图象与一次函数 的图象的交点为A(m,2). (1)、求一次函数的解析式;(2)、观察图像直接写出使得 的 的取值范围;23. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)、求一次函数的解析式;(2)、观察图像直接写出使得 的 的取值范围;23. 已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD. (1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.24. 京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.(1)、求甲、乙两队单独完成这项工程各需多少天?(2)、已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.25. 如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD= ,DF= .
(1)、求证:四边形AODE是矩形;(2)、若AB=6,∠BCD=120°,求四边形AODE的面积.24. 京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.(1)、求甲、乙两队单独完成这项工程各需多少天?(2)、已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.25. 如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD= ,DF= . (1)、求 与 的函数关系式;(2)、当四边形AEFD为菱形时,求 的值;(3)、当△FED是直角三角形时,求 的值.26. 如图,正方形AOCB在平面直角坐标系 中,点O为原点,点B在反比例函数 ( > )图象上,△BOC的面积为 .
(1)、求 与 的函数关系式;(2)、当四边形AEFD为菱形时,求 的值;(3)、当△FED是直角三角形时,求 的值.26. 如图,正方形AOCB在平面直角坐标系 中,点O为原点,点B在反比例函数 ( > )图象上,△BOC的面积为 . (1)、求反比例函数 的关系式;(2)、若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F 从B开始沿BC向C以每秒 个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用 表示,△BEF的面积用 表示,求出 关于 的函数关系式,并求出当运动时间 取何值时,△BEF的面积最大?(3)、当运动时间为 秒时,在坐标轴上是否存在点P,使得△PEF的周长最小?若存在,请求出点P的坐标;若不存在请说明理由.27. 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),
(1)、求反比例函数 的关系式;(2)、若动点E从A开始沿AB向B以每秒1个单位的速度运动,同时动点F 从B开始沿BC向C以每秒 个单位的速度运动,当其中一个动点到达端点时,另一个动点随之停止运动.若运动时间用 表示,△BEF的面积用 表示,求出 关于 的函数关系式,并求出当运动时间 取何值时,△BEF的面积最大?(3)、当运动时间为 秒时,在坐标轴上是否存在点P,使得△PEF的周长最小?若存在,请求出点P的坐标;若不存在请说明理由.27. 已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0), (1)、求过点A,B的直线的函数表达式;(2)、在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(3)、在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.
(1)、求过点A,B的直线的函数表达式;(2)、在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(3)、在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.