吉林省长春六中、八中、十一中等省重点中学2019-2020学年高三理数12月联考试卷
试卷更新日期:2020-01-13 类型:月考试卷
一、单选题
-
1. 若集合 , ,则 ( )A、 B、 C、 D、2. 若实数 , 满足 , ,则 的取值范围是( )A、 B、 C、 D、3. 若 ,则下列不等式中恒成立的是( )A、 B、 C、 D、4. 关于“ ,则 , 至少有一个等于 ”及其逆命题的说法正确的是( )A、原命题为真,逆命题为假 B、原命题为假,逆命题为真 C、原命题与逆命题均为真命题 D、原命题与逆命题均为假命题5. 若数列 中的项按一定规律变化,则实数 最有可能的值是( )A、 B、 C、 D、6. 已知平面向量 , ,若 ,则 ( )A、 B、 C、 D、7. 若实数 , 满足 ,则 的最小值是( )A、 B、 C、 D、8. 若实数 , 满足不等式组 ,则 的最大值为( )A、 B、 C、 D、9. 已知二次函数 满足 ,若 在区间 上单调递减,且 恒成立,则实数 的取值范围是( )A、 B、 C、 D、10. 已知数列 的前 项和 , 则数列 的前 项和 满足( )A、 B、 C、 D、11. 函数 的图像大致为( )A、
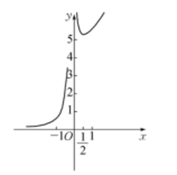 B、
B、 C、
C、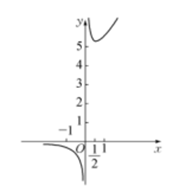 D、
D、 12. 下列表述正确的是( )
12. 下列表述正确的是( )① ;②若 ,则 ;③若 , , 均是正数,且 , ,则 的值是 ;④若正实数 , 满足 ,且 ,则 , 均为定值
A、①②③ B、②④ C、②③ D、②③④二、填空题
-
13. 若数列 满足 , ,则 .14. 若函数 ,则不等式 的解集是 .15. 已知函数 满足 ,若 ,则不等式 的解集为 .16. 已知以区间 上的整数为分子,以 为分母的数组成集合 ,其所有元素的和为 ;以区间 上的整数为分子,以 为分母组成不属于集合 的数组成集合 ,其所有元素的和为 ;……依此类推以区间 上的整数为分子,以 为分母组成不属于 , … 的数组成集合 ,其所有元素的和为 ,若数列 前 项和为 ,则 .
三、解答题
-
17. 已知函数 .(1)、若当 时,函数 的值域为 ,求实数 , 的值;(2)、在(1)条件下,求函数 图像的对称中心.18. 已知函数(1)、若函数 的值域为 ,求实数 的值;(2)、若 对任意的 成立,求实数 的取值范围。19. 已知各项均为正数的等比数列 的首项为 ,且 。(1)、求数列 的通项公式;(2)、若 ,数列 的前 项和为 ,数列 的前 项和为 ,试比较 与 的大小.