广西名校2019-2020学年高三上学期理数12月高考模拟试卷
试卷更新日期:2020-01-13 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则P的非空子集的个数是( )A、7 B、15 C、63 D、642. 定义运算 ,若 ,则复数 对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图是国家统计局今年4月11日发布的2018年3月到2019年3月全国居民消费价格的涨跌幅情况折线图.(注:2019年2月与2018年2月相比较称同比,2019年2月与2019年1月相比较称环比),根据该折线图,下列结论错误的是( )
 A、2018年3月至2019年3月全国居民消费价格同比均上涨 B、2018年3月至2019年3月全国居民消费价格环比有涨有跌 C、2019年3月全国居民消费价格同比涨幅最大 D、2019年3月全国居民消费价格环比变化最快4. 的展开式中 的系数为( )A、320 B、300 C、280 D、2605. 我国明代伟大数学家程大位在《算法统宗》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上梢四节贮三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”意思是:九节竹的盛米容积成等差数列,其中的“三升九”指3.9升,则九节竹的中间一节的盛米容积为( )A、0.9升 B、1升 C、1.1升 D、2.1升6. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( )
A、2018年3月至2019年3月全国居民消费价格同比均上涨 B、2018年3月至2019年3月全国居民消费价格环比有涨有跌 C、2019年3月全国居民消费价格同比涨幅最大 D、2019年3月全国居民消费价格环比变化最快4. 的展开式中 的系数为( )A、320 B、300 C、280 D、2605. 我国明代伟大数学家程大位在《算法统宗》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上梢四节贮三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”意思是:九节竹的盛米容积成等差数列,其中的“三升九”指3.9升,则九节竹的中间一节的盛米容积为( )A、0.9升 B、1升 C、1.1升 D、2.1升6. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( ) A、 B、 C、6 D、7. 已知函数 ,则 的图象大致为( )A、
A、 B、 C、6 D、7. 已知函数 ,则 的图象大致为( )A、 B、
B、 C、
C、 D、
D、 8. 如图所给的程序运行结果为 ,那么判断框中应填入的关于 的条件是( )
8. 如图所给的程序运行结果为 ,那么判断框中应填入的关于 的条件是( )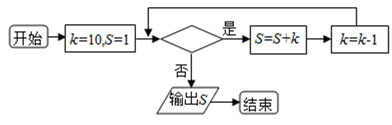 A、 B、 C、 D、9. 已知点 是抛物线 上的一动点, 为抛物线的焦点, 是圆 : 上一动点,则 的最小值为( )A、3 B、4 C、5 D、610. 过双曲线 的右顶点 作斜率为 的直线,该直线与双曲线的两条渐近线的交点分别为 .若 ,则双曲线的离心率是 ( )A、 B、 C、 D、11. 已知函数 满足 ,且当 时, 成立,若 , , ,则a,b,c的大小关系是( )A、a B、 C、 D、c12. 已知半径为2的扇形AOB中, ,C是OB的中点,P为弧AB上任意一点,且 ,则 的最大值为( )A、2 B、 C、 D、
A、 B、 C、 D、9. 已知点 是抛物线 上的一动点, 为抛物线的焦点, 是圆 : 上一动点,则 的最小值为( )A、3 B、4 C、5 D、610. 过双曲线 的右顶点 作斜率为 的直线,该直线与双曲线的两条渐近线的交点分别为 .若 ,则双曲线的离心率是 ( )A、 B、 C、 D、11. 已知函数 满足 ,且当 时, 成立,若 , , ,则a,b,c的大小关系是( )A、a B、 C、 D、c12. 已知半径为2的扇形AOB中, ,C是OB的中点,P为弧AB上任意一点,且 ,则 的最大值为( )A、2 B、 C、 D、二、填空题
-
13. 已知向量 , , , ,若 ,则 的最小值 .14. 若数列 的首项 ,且 ;令 ,则 .15. 在锐角 中, , , ,则 .16. 在三棱锥 中,面 面 , , , 则三棱锥 的外接球的表面积是
三、解答题
-
17. 已知数列 的前n项和 ,其中 .(1)、证明 是等比数列,并求其通项公式;(2)、若 ,求 .18. 为推进“千村百镇计划”, 年 月某新能源公司开展“电动莆田 绿色出行”活动,首批投放 台 型新能源车到莆田多个村镇,供当地村民免费试用三个月.试用到期后,为了解男女试用者对 型新能源车性能的评价情况,该公司要求每位试用者填写一份性能综合评分表(满分为 分).最后该公司共收回 份评分表,现从中随机抽取 份(其中男、女的评分表各 份)作为样本,经统计得到如下茎叶图:
 (1)、求 个样本数据的中位数 ;(2)、已知 个样本数据的平均数 ,记 与 的最大值为 .该公司规定样本中试用者的“认定类型”:评分不小于 的为“满意型”,评分小于 的为“需改进型”.
(1)、求 个样本数据的中位数 ;(2)、已知 个样本数据的平均数 ,记 与 的最大值为 .该公司规定样本中试用者的“认定类型”:评分不小于 的为“满意型”,评分小于 的为“需改进型”.①请根据 个样本数据,完成下面 列联表:

根据 列联表判断能否有 的把握认为“认定类型”与性别有关?
②为做好车辆改进工作,公司先从样本“需改进型”的试用者按性别用分层抽样的方法,从中抽取8人进行回访,根据回访意见改进车辆后,再从这8人中随机抽取3人进行二次试用,记这3人中男性人数为 ,求 的分布列及数学期望.
19. 如图,正方体 的棱长为2,P是BC的中点,点Q是棱 上的动点. (1)、点Q在何位置时,直线 ,DC,AP交于一点,并说明理由;(2)、求三棱锥 的体积;(3)、棱 上是否存在动点Q,使得 与平面 所成角的正弦值为 ,若存在指出点Q在棱 上的位置,若不存在,请说明理由.20. 如图,中心为坐标原点O的两圆半径分别为 , ,射线OT与两圆分别交于A、B两点,分别过A、B作垂直于x轴、y轴的直线 、 , 交 于点P.
(1)、点Q在何位置时,直线 ,DC,AP交于一点,并说明理由;(2)、求三棱锥 的体积;(3)、棱 上是否存在动点Q,使得 与平面 所成角的正弦值为 ,若存在指出点Q在棱 上的位置,若不存在,请说明理由.20. 如图,中心为坐标原点O的两圆半径分别为 , ,射线OT与两圆分别交于A、B两点,分别过A、B作垂直于x轴、y轴的直线 、 , 交 于点P. (1)、当射线OT绕点O旋转时,求P点的轨迹E的方程;(2)、直线l: 与曲线E交于M、N两点,两圆上共有6个点到直线l的距离为 时,求 的取值范围.
(1)、当射线OT绕点O旋转时,求P点的轨迹E的方程;(2)、直线l: 与曲线E交于M、N两点,两圆上共有6个点到直线l的距离为 时,求 的取值范围.