山东省蒙阴县2016-2017学年七年级下学期期末考试数学试题
试卷更新日期:2017-08-04 类型:期末考试
一、选择题
-
1. 在实数-3、0、 、3中,最小的实数是( )A、-3 B、0 C、 D、32. 64的立方根是( )A、8 B、±8 C、4 D、±43. 点A(﹣2,﹣3)所在象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )A、
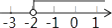 B、
B、 C、
C、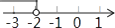 D、
D、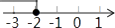 5. 在1000个数据中,用适当的方法抽取50个作为样本进行统计,频数分布表中54.5~57.5这一组的频率是0.12,那么个体数据落在54.5~57.5之间的约有( ).A、120个 B、60个 C、12个 D、6个6. 如图,下列条件中,不能判断直线l1∥l2的是( )
5. 在1000个数据中,用适当的方法抽取50个作为样本进行统计,频数分布表中54.5~57.5这一组的频率是0.12,那么个体数据落在54.5~57.5之间的约有( ).A、120个 B、60个 C、12个 D、6个6. 如图,下列条件中,不能判断直线l1∥l2的是( ) A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°7. 若 是同类项,则a﹣b的值是( )A、0 B、1 C、2 D、38.
A、∠1=∠3 B、∠2=∠3 C、∠4=∠5 D、∠2+∠4=180°7. 若 是同类项,则a﹣b的值是( )A、0 B、1 C、2 D、38.如图,AB∥CD∥EF , AF∥CG , 则图中与∠F(不包括∠F)相等的角有( )
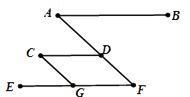 A、1个 B、2个 C、3个 D、4个9. 已知实数 , 满足 ,则 等于( )A、3 B、-3 C、1 D、-110. 在平面直角坐标系中,将点(2,3)向上平移1个单位,再向左平移2个单位,所得到的点的坐标是( )A、(-2,3) B、(-1,2) C、(0,4) D、(4,4)11. 不等式组 的正整数解的个数是( )A、1 B、2 C、3 D、412.
A、1个 B、2个 C、3个 D、4个9. 已知实数 , 满足 ,则 等于( )A、3 B、-3 C、1 D、-110. 在平面直角坐标系中,将点(2,3)向上平移1个单位,再向左平移2个单位,所得到的点的坐标是( )A、(-2,3) B、(-1,2) C、(0,4) D、(4,4)11. 不等式组 的正整数解的个数是( )A、1 B、2 C、3 D、412.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a,b的值分别为( )
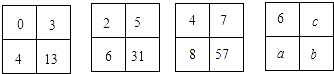 A、9,10 B、9,91 C、10,91 D、10,110
A、9,10 B、9,91 C、10,91 D、10,110二、填空题
-
13.
已知 、
 为两个连续的整数,且 < <
为两个连续的整数,且 < <  ,则 . 14. 若 , ,则x+y的值是 .15. 在扇形统计图中,其中一个扇形的圆心角是216°,则这个扇形所表示的部分占总体的百分数是.16.
,则 . 14. 若 , ,则x+y的值是 .15. 在扇形统计图中,其中一个扇形的圆心角是216°,则这个扇形所表示的部分占总体的百分数是.16.如图所示,两块三角尺的直角顶点 重叠在一起,且 恰好平分 ,则 的度数是.
 17. 不等式: 的非正整数解个数有个.18. 对于有理数,规定新运算:x※y=ax+by+xy , 其中a 、b是常数,等式右边的是通常的加法和乘法运算. 已知:2※1=7 ,(-3)※3=3 ,则 ※b=.
17. 不等式: 的非正整数解个数有个.18. 对于有理数,规定新运算:x※y=ax+by+xy , 其中a 、b是常数,等式右边的是通常的加法和乘法运算. 已知:2※1=7 ,(-3)※3=3 ,则 ※b=.三、解答题
-
19. 综合题(1)、计算:|﹣ |﹣ -| -2|;(2)、解方程:20.
解不等式组: ,并把解集在数轴上表示出来.
 21.
21.某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味,草莓味,菠萝味,香橙味,核桃味五种口味的牛奶供学生饮用,海马中学为了了解学生对不同口味的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同,绘制了如下两张不完整的人数统计图)
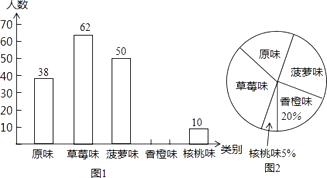 (1)、本次被调查的学生有名(2)、补全上面的条形统计图,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数.(3)、该校共有1200名学生订购了该品牌的牛奶.牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都能喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味比原味多送多少盒?22.
(1)、本次被调查的学生有名(2)、补全上面的条形统计图,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数.(3)、该校共有1200名学生订购了该品牌的牛奶.牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都能喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味比原味多送多少盒?22.如图,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2,∠3=80°.
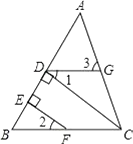 (1)、试证明∠B=∠ADG;(2)、求∠BCA的度数.23.
(1)、试证明∠B=∠ADG;(2)、求∠BCA的度数.23.如图,△ABC在直角坐标系中,
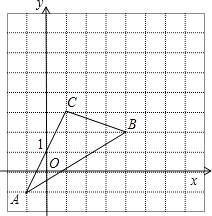 (1)、请写出△ABC各点的坐标;(2)、求出S△ABC;(3)、若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.24. 双蓉服装店老板到厂家购A、B两种型号的服装,若购A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元。(1)、求A、B两种型号的服装每件分别为多少元?(2)、若销售一件A型服装可获利18元,销售一件B型服装可获利30元,根据市场需要,服装店老板决定:购进A型服装的数量要比购进B型服装的数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后可使总的获利不少于699元,问有几种进货方案?如何进货?25.
(1)、请写出△ABC各点的坐标;(2)、求出S△ABC;(3)、若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.24. 双蓉服装店老板到厂家购A、B两种型号的服装,若购A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B种型号服装8件,需要1880元。(1)、求A、B两种型号的服装每件分别为多少元?(2)、若销售一件A型服装可获利18元,销售一件B型服装可获利30元,根据市场需要,服装店老板决定:购进A型服装的数量要比购进B型服装的数量的2倍还多4件,且A型服装最多可购进28件,这样服装全部售出后可使总的获利不少于699元,问有几种进货方案?如何进货?25.如图(1),E是直线AB、CD内部一点,AB∥CD , 连接EA、ED.
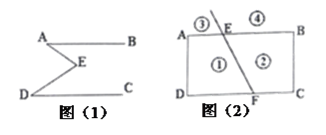 (1)、探究猜想:
(1)、探究猜想:①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图(1)中∠AED、∠EAB、∠EDC的关系并证明你的结论.
(2)、拓展应用:如图(1),射线FE与矩形ABCD的边AB交于点E , 与边CD交于点F , ①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③④位于直线AB上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF的关系(不要求证明).