内蒙古赤峰市宁城县2016-2017学年七年级下学期期末考试数学试题
试卷更新日期:2017-08-04 类型:期末考试
一、选择题
-
1. 下列几个汽车的车标图案中,可以看做是由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各数中,3.14159,- ,0.131131113…,-π, ,- ,无理数的个数有( )
2. 下列各数中,3.14159,- ,0.131131113…,-π, ,- ,无理数的个数有( )
A、1个 B、2个 C、3个 D、4个3.如图是我们生活中经常接触的小刀,刀片的外壳是四边形,而且刀片外壳与刀片铆合部分都是直角,刀片的上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2的度数为( )
 A、80° B、70° C、90° D、100°4. 下列语句写成式子正确的是 ( )A、4是16的平方根,即 =4 B、4是(-4)2的算术平方根,即 =4 C、±4是16的平方根,即± =4 D、±4是16的平方根,即 =±45. 下列调查方式科学合理的是( )A、对某校七年级一班全体同学喜爱球类运动的情况进行调查,采用抽样调查的方式. B、了解赤峰市九年级同学的视力情况,采用全面调查的方式. C、某农田保护区对区内的小麦的高度进行调查,采用全面调查的方式. D、对宁城县食品合格情况的调查,采用抽样调查的方式.6. 若a2=25,|b|=3,且ab>0,则a+b的值为( )A、8 B、-8 C、8或-8 D、8或-27. 点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )A、4cm B、2cm C、小于2cm D、不大于2cm8. 在平面直角坐标系中,点P(-3,b)到x轴的距离为4,则P点坐标为( )A、(-3,4) B、(-3,-4) C、(-3,4)或(-3,-4) D、(3,4)或(3,-4)9. 小明和小莉出生于1998年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是22,那么小莉的出生日期是( )A、15号 B、16号 C、17号 D、18号10. 已知点p(3-m,m-1)在第二象限,则m的取值范围在数轴上表示正确的是( )
A、80° B、70° C、90° D、100°4. 下列语句写成式子正确的是 ( )A、4是16的平方根,即 =4 B、4是(-4)2的算术平方根,即 =4 C、±4是16的平方根,即± =4 D、±4是16的平方根,即 =±45. 下列调查方式科学合理的是( )A、对某校七年级一班全体同学喜爱球类运动的情况进行调查,采用抽样调查的方式. B、了解赤峰市九年级同学的视力情况,采用全面调查的方式. C、某农田保护区对区内的小麦的高度进行调查,采用全面调查的方式. D、对宁城县食品合格情况的调查,采用抽样调查的方式.6. 若a2=25,|b|=3,且ab>0,则a+b的值为( )A、8 B、-8 C、8或-8 D、8或-27. 点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )A、4cm B、2cm C、小于2cm D、不大于2cm8. 在平面直角坐标系中,点P(-3,b)到x轴的距离为4,则P点坐标为( )A、(-3,4) B、(-3,-4) C、(-3,4)或(-3,-4) D、(3,4)或(3,-4)9. 小明和小莉出生于1998年12月份,他们的出生日不是同一天,但都是星期五,且小明比小莉出生早,两人出生日期之和是22,那么小莉的出生日期是( )A、15号 B、16号 C、17号 D、18号10. 已知点p(3-m,m-1)在第二象限,则m的取值范围在数轴上表示正确的是( )
A、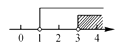 B、
B、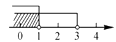 C、
C、 D、
D、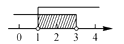 11. 如果不等式组 的解集是x<2,那么m的取值范围是( )A、m=2 B、m>2 C、m<2 D、m≥212. 某种商品价格为33元/件,某人只带有2元和5元的两种面值的购物券各若干张,买了一件这种商品;若无需找零钱,则付款方式中张数之和(指付2元和5元购物券的张数)最少和张数之和最多的方式分别是( )A、8张和16张 B、8张和15张 C、9张和16张 D、9张和15张
11. 如果不等式组 的解集是x<2,那么m的取值范围是( )A、m=2 B、m>2 C、m<2 D、m≥212. 某种商品价格为33元/件,某人只带有2元和5元的两种面值的购物券各若干张,买了一件这种商品;若无需找零钱,则付款方式中张数之和(指付2元和5元购物券的张数)最少和张数之和最多的方式分别是( )A、8张和16张 B、8张和15张 C、9张和16张 D、9张和15张二、填空题
-
13. 以下五个条件中,能得到互相垂直关系的有 . (填写序号)
①对顶角的平分线;②邻补角的平分线;③平行线截得的一组同位角的平分线;④平行线截得的一组内错角的平分线;⑤平行线截得的一组同旁内角的平分线.
14. 若 , ,则 = .15. 若 是关于a,b的二元一次方程ax+ay-b=7的一个解,则代数式x2+2xy+y2-1的值是 .16.⑴两条直线相交于一点有2组不同的对顶角;
⑵三条直线相交于一点有6组不同的对顶角;
⑶四条直线相交于一点有12组不同的对顶角;
⑷n条直线相交于同一点有组不同对顶角.(如图所示)

三、解答题
-
17. 计算: 2 +|- |-(-1)2017+2;18. 解方程组:19.
如图,完成下列推理过程.
已知:DE⊥AO于E,BO⊥AO,∠CFB=∠EDO.
求证:CF∥DO.

证明:∵DE⊥AO,BO⊥AO(已知)
∴∠DEA=∠BOA=90°()
∴DE∥BO()
∴∠EDO=∠DOF()
又∵∠CFB=∠EDO()
∴∠DOF=∠CFB()
∴CF∥DO()
20. 已知关于x、y的方程组 的解适合不等式2x-y>3,求a的取值范围.21. 如图,在单位正方形网格中,建立了平面直角坐标系xOy,试解答下列问题: (1)、写出三角形ABC三个顶点的坐标;(2)、画出三角形ABC向右平移6个单位,再向下平移2个单位后的图形三角形DEF;(3)、若点P(a,b)是三角形ABC内部一点,求平移后三角形A , B , C , 内的对应点P , 的坐标.
(1)、写出三角形ABC三个顶点的坐标;(2)、画出三角形ABC向右平移6个单位,再向下平移2个单位后的图形三角形DEF;(3)、若点P(a,b)是三角形ABC内部一点,求平移后三角形A , B , C , 内的对应点P , 的坐标.
(4)、求三角形DEF的面积.22. 某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题:
 (1)、此次抽样调查的样本容量是;(2)、补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;(3)、如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?23.
(1)、此次抽样调查的样本容量是;(2)、补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数;(3)、如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?23.如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
 (1)、求∠DAB的度数,并写出理由.(2)、求∠EAC的度数.(3)、计算∠BAC的度数.(4)、根据以上条件及结论,你还能得出其他结论吗?试写出一个.24. 对于实数x,规定 表示不小于x的最小整数,例如 , , ,则(1)、填空:① ;
(1)、求∠DAB的度数,并写出理由.(2)、求∠EAC的度数.(3)、计算∠BAC的度数.(4)、根据以上条件及结论,你还能得出其他结论吗?试写出一个.24. 对于实数x,规定 表示不小于x的最小整数,例如 , , ,则(1)、填空:① ;②若 ,则x的取值范围是.
(2)、已知x为正整数,且 ,求 的值.25.有一天李明同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图一),他用鼠标左键点住点E,拖动后,分别得到如图二,三,四等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着李明同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
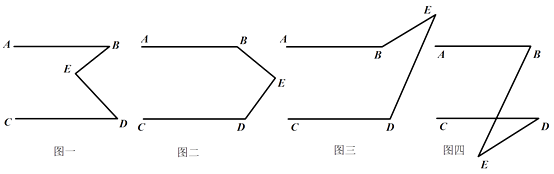 (1)、你能探究出图一到图四各图中的∠B,∠D与∠BED之间的关系吗?(2)、请从所得的四个关系中,选一个说明它成立的理由.26. 某校组织夏令营活动,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则刚好坐满;若只租用42座客车,则能少租一辆,而且还有一辆没有坐满,但超过30人,问:(1)、该校有多少人参加夏令营活动?(2)、已知36座客车每辆租金400元,42座客车每辆租金440元,请你帮该校设计一种最省钱得租车方案。
(1)、你能探究出图一到图四各图中的∠B,∠D与∠BED之间的关系吗?(2)、请从所得的四个关系中,选一个说明它成立的理由.26. 某校组织夏令营活动,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则刚好坐满;若只租用42座客车,则能少租一辆,而且还有一辆没有坐满,但超过30人,问:(1)、该校有多少人参加夏令营活动?(2)、已知36座客车每辆租金400元,42座客车每辆租金440元,请你帮该校设计一种最省钱得租车方案。