初中数学浙教版七年级下册第一章 平行线 章末检测
试卷更新日期:2020-01-10 类型:单元试卷
一、单选题
-
1. 下列四个图形中,可以由下图通过平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. ∠B的同位角可以是( ).
2. ∠B的同位角可以是( ).
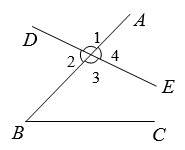
A、∠1 B、∠2 C、∠3 D、∠43. 如图,不能作为判断AE∥CD的条件的是( )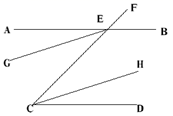 A、∠FEB=∠ECD B、∠AEC=∠ECD C、∠BEC+∠ECD=180° D、∠AEG=∠DCH4. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、
A、∠FEB=∠ECD B、∠AEC=∠ECD C、∠BEC+∠ECD=180° D、∠AEG=∠DCH4. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,直线 , ,则 ( )
5. 如图,直线 , ,则 ( ) A、150° B、180° C、210° D、240°6. 如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠α=135°,则∠β等于( )
A、150° B、180° C、210° D、240°6. 如图,将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上,若∠α=135°,则∠β等于( )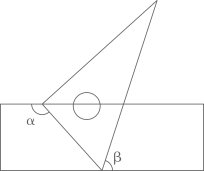 A、45° B、60° C、75° D、85°7. 如图, 是由 沿BD所在的直线平移得到的,AE,BF的延长线交于点C,若 ,则 的度数是
A、45° B、60° C、75° D、85°7. 如图, 是由 沿BD所在的直线平移得到的,AE,BF的延长线交于点C,若 ,则 的度数是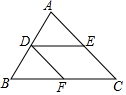 A、
A、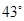 B、
B、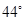 C、
C、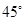 D、
D、 8. 如图,将边长为5个单位的等边△ABC沿边BC向右平移4个单位得到△A’B’C’,则四边形AA’C’B的周长为( )
8. 如图,将边长为5个单位的等边△ABC沿边BC向右平移4个单位得到△A’B’C’,则四边形AA’C’B的周长为( )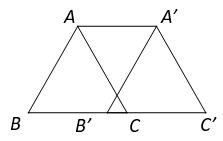 A、22cm B、23cm C、24cm D、25cm9. 在同一平面内,两条直线的位置关系有( )
A、22cm B、23cm C、24cm D、25cm9. 在同一平面内,两条直线的位置关系有( )
A、两种:平行和相交 B、两种:平行和垂直 C、三种:平行、垂直和相交 D、两种:相交和垂直10. 如图,将△ABC向右平移5个单位长度得到△DEF,且点B,E,C,F在同一条直线上.若EC= ,则BC的长度是( ) A、8 B、9 C、10 D、11
A、8 B、9 C、10 D、11二、填空题
-
11. 如图,能与∠1构成同位角的角有个.
 12. 如图,若要 ,需增加条件.(填一个即可)
12. 如图,若要 ,需增加条件.(填一个即可)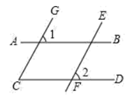 13. 阅读下面材料:在数学课上,老师提出如下问题:
13. 阅读下面材料:在数学课上,老师提出如下问题:作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A(如图1).
求作:l的平行线,使它经过点A .
小凡利用两块形状相同的三角尺进行如下操作:
如图2所示:
⑴用第一块三角尺的一条边贴住直线l , 第二块三角尺的一条边紧靠第一块三角尺;
⑵将第二块三角尺沿第一块三角尺移动,使其另一边经过点A , 沿这边作出直线AB , 所以,直线AB即为所求.
老师说:“小凡的作法正确”
请回答:小凡的作图依据是 .
 14. 如图,AB∥EF,若∠C=90°,那么x、y和z的关系是
14. 如图,AB∥EF,若∠C=90°,那么x、y和z的关系是 15. 如图,Rt△ABC中,AC=5,BC=12,AB=13,则其内部五个小直角三角形的周长之和为.
15. 如图,Rt△ABC中,AC=5,BC=12,AB=13,则其内部五个小直角三角形的周长之和为.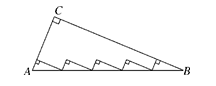 16. 如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动格.
16. 如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动格.
三、解答题
-
17. 如图,直线AD与AE相交于点A,直线BC分别交AD、AE于点B、C,直线DE分别交AD、AE于点D、E,分别写出图中的两对同位角、两对内错角、两对同旁内角.
 18. 如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?
18. 如图,张三打算在院落里种上蔬菜,已知院落为东西长32 m,南北宽20 m的长方形,为了行走方便,要修筑同样宽的三条道路:东西两条,南北一条,南北道路垂直于东西道路,余下的部分要分别种上西红柿、青椒、菜豆、黄瓜等蔬菜,若每条道路的宽均为1 m,求蔬菜的总种植面积是多少?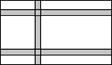 19. 如图:
19. 如图: (1)、如果∠1= , 那么DE∥AC,理由: .(2)、如果∠1= , 那么EF∥BC,理由: .(3)、如果∠FED+∠EFC=180°,那么 , 理由: .(4)、如果∠2+∠AED=180°,那么 , 理由: .20. 如图,已知 DC∥FP , ,FH平分 .
(1)、如果∠1= , 那么DE∥AC,理由: .(2)、如果∠1= , 那么EF∥BC,理由: .(3)、如果∠FED+∠EFC=180°,那么 , 理由: .(4)、如果∠2+∠AED=180°,那么 , 理由: .20. 如图,已知 DC∥FP , ,FH平分 .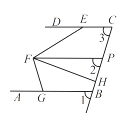 (1)、说明: ;(2)、求 的度数.21. 问题情境:在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
(1)、说明: ;(2)、求 的度数.21. 问题情境:在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.

(1)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;(2)、结论应用
如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于(用含α的式子表示).
22. 如图,在 网格中,已知△ABC,请按下列要求画格点三角形 (三角形的三个顶点都是小正方形的顶点).
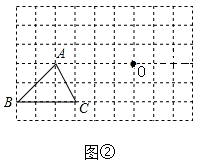 (1)、在图①中,将△ABC平移,使点O落在△ABC的边AB(不包括点A和点B)上;(2)、在图②中,将△ABC平移,使点O落在△ABC的内部.
(1)、在图①中,将△ABC平移,使点O落在△ABC的边AB(不包括点A和点B)上;(2)、在图②中,将△ABC平移,使点O落在△ABC的内部.