黑龙江省哈尔滨市香坊区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2020-01-09 类型:期末考试
一、单选题
-
1. 点P(3,5)关于原点对称的点的坐标是( )A、(﹣3,5) B、(3,﹣5) C、(5,3) D、(﹣3,﹣5)2. 下列图形中,是中心对称图形的是( )A、
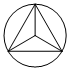 B、
B、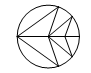 C、
C、 D、
D、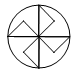 3. 在 中, , ,则 ( )A、 B、 C、 D、4. 如图所示的几何体的主视图是
3. 在 中, , ,则 ( )A、 B、 C、 D、4. 如图所示的几何体的主视图是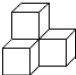 A、
A、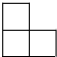 B、
B、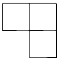 C、
C、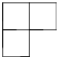 D、
D、 5. 对于双曲线 ,当 时, 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、6. 把抛物线 向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )A、 B、 C、 D、7. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
5. 对于双曲线 ,当 时, 随 的增大而增大,则 的取值范围是( )A、 B、 C、 D、6. 把抛物线 向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )A、 B、 C、 D、7. 如图,将△ABC绕点C顺时针旋转90°得到△EDC . 若点A , D , E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )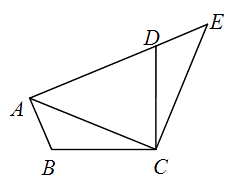 A、55° B、60° C、65° D、70°8. 下列命题是真命题的是( )A、直径是圆中最长的弦 B、三个点确定一个圆 C、平分弦的直径垂直于弦 D、相等的圆心角所对的弦相等9. 如图,点 是平行四边形 的边 上一点,射线 交 的延长线于点 ,则下列结论错误的是( )
A、55° B、60° C、65° D、70°8. 下列命题是真命题的是( )A、直径是圆中最长的弦 B、三个点确定一个圆 C、平分弦的直径垂直于弦 D、相等的圆心角所对的弦相等9. 如图,点 是平行四边形 的边 上一点,射线 交 的延长线于点 ,则下列结论错误的是( ) A、 B、 C、 D、10. 如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
A、 B、 C、 D、10. 如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.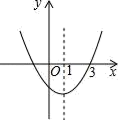 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
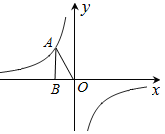
11. 在 中, , , ,则 =度。12. 抛物线 的顶点坐标是。13. 小明掷一枚均匀的骰子,骰子的六个面上分别刻有1,2,3,4,5,6点,得到的点数为奇数的概率是 .14. 如图,已知反比例函数y= (k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B,若△AOB的面积为1,则k= .
 15. 上午某一时刻,身高1.7米的小刚在地面上的影长为3.4米,则影长26米的旗轩高度为米16. 某扇形的弧长是 ,半径是5cm , 则此扇形的圆心角是度17. 如图, 是⊙ 的弦,⊙ 的半径为5, 于 ,交⊙ 于 ,且 ,则 长为。
15. 上午某一时刻,身高1.7米的小刚在地面上的影长为3.4米,则影长26米的旗轩高度为米16. 某扇形的弧长是 ,半径是5cm , 则此扇形的圆心角是度17. 如图, 是⊙ 的弦,⊙ 的半径为5, 于 ,交⊙ 于 ,且 ,则 长为。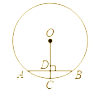 18. 如图,在平行四边形ABCD中, 于点E , 于点F , 若 , , ,则平行四边形ABCD的面积为 .
18. 如图,在平行四边形ABCD中, 于点E , 于点F , 若 , , ,则平行四边形ABCD的面积为 .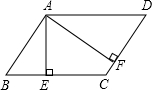 19. 如图 中, , , 中, , ,点D在线段AC上,点E在段BC的延长线上,将 绕点C旋转 得到 ,则 .
19. 如图 中, , , 中, , ,点D在线段AC上,点E在段BC的延长线上,将 绕点C旋转 得到 ,则 .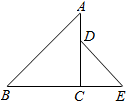
三、解答题
-
20. 如图,从热气球C上测得两建筑物A,B底部的俯角分别为30°和60度.如果这时气球的高度CD为90米.且点A,D,B在同一直线上,求建筑物A,B间的距离.
 21. 先化简再求值: ÷(a﹣ ),其中a=2cos30°+1,b=tan45°.22. 如图的方格纸中每个小正方形的边长均为1,线段AB的两个端点均在格点上;
21. 先化简再求值: ÷(a﹣ ),其中a=2cos30°+1,b=tan45°.22. 如图的方格纸中每个小正方形的边长均为1,线段AB的两个端点均在格点上;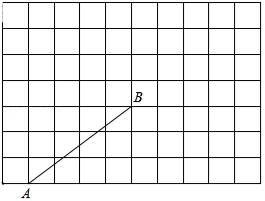 (1)、在图中画出以AB为腰,面积为7.5的等腰△ABC , 且点C在格点上;(2)、在图中画出平行四边形ABDE , 且点D、E均在格点上,使tan∠EAC= ,连接CD , 请直接写出线段CD的长.23. 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行100米跑步测试,按照成绩分为优秀、良好、合格与不合格四个等级,其中不合格学生占抽取学生总数的 ,学校绘制了如下不完整的统计图:
(1)、在图中画出以AB为腰,面积为7.5的等腰△ABC , 且点C在格点上;(2)、在图中画出平行四边形ABDE , 且点D、E均在格点上,使tan∠EAC= ,连接CD , 请直接写出线段CD的长.23. 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行100米跑步测试,按照成绩分为优秀、良好、合格与不合格四个等级,其中不合格学生占抽取学生总数的 ,学校绘制了如下不完整的统计图: (1)、通过计算补全条形统计图;(2)、校九年级有300名男生,请估计其中成绩未达到良好和优秀的有多少?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米跑步比赛、预赛分为A、B、C三组进行,选手由抽签确定分组,甲、乙两人恰好分在同一组的概率是多少?请画出树状图或列表加以说明.24. 如图,PA切⊙O于点A,射线PC交⊙O于C、B两点,半径OD⊥BC于E,连接BD、DC和OA,DA交BP于点F;
(1)、通过计算补全条形统计图;(2)、校九年级有300名男生,请估计其中成绩未达到良好和优秀的有多少?(3)、某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米跑步比赛、预赛分为A、B、C三组进行,选手由抽签确定分组,甲、乙两人恰好分在同一组的概率是多少?请画出树状图或列表加以说明.24. 如图,PA切⊙O于点A,射线PC交⊙O于C、B两点,半径OD⊥BC于E,连接BD、DC和OA,DA交BP于点F;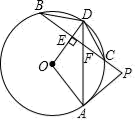 (1)、求证:∠ADC+∠CBD= ∠AOD;(2)、在不添加任何辅助线的情况下,请直接写出图中相等的线段.25. 童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销该店决定降价销售,经市场调查发现:每降价1元,每星期可多卖10件,已知该款童装每件成本30元,设降价后该款童装每件售价 元,每星期的销售量为 件.(1)、降价后,当某一星期的销售量是未降价前一星期销售量的3倍时,求这一星期中每件童装降价多少元?(2)、当每件售价定为多少元时,一星期的销售利润最大,最大利润是多少?26. 已知:在 中,C、D分别为BM、AM上的点,四边形ABCD内接于 ,连接AC , ;
(1)、求证:∠ADC+∠CBD= ∠AOD;(2)、在不添加任何辅助线的情况下,请直接写出图中相等的线段.25. 童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销该店决定降价销售,经市场调查发现:每降价1元,每星期可多卖10件,已知该款童装每件成本30元,设降价后该款童装每件售价 元,每星期的销售量为 件.(1)、降价后,当某一星期的销售量是未降价前一星期销售量的3倍时,求这一星期中每件童装降价多少元?(2)、当每件售价定为多少元时,一星期的销售利润最大,最大利润是多少?26. 已知:在 中,C、D分别为BM、AM上的点,四边形ABCD内接于 ,连接AC , ;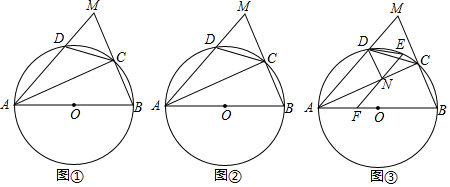 (1)、如图①,求证:弧 弧BD;(2)、如图②,若AB为直径, ,求 值;(3)、如图③,在 的条件下,E为弧CD上一点 不与C、D重合 ,F为AB上一点,连接EF交AC于点N , 连接DN、DE , 若 , , ,求AN的长.27. 如图抛物线y=ax2+2交x轴于点A(﹣2,0)、B,交y轴于点C;
(1)、如图①,求证:弧 弧BD;(2)、如图②,若AB为直径, ,求 值;(3)、如图③,在 的条件下,E为弧CD上一点 不与C、D重合 ,F为AB上一点,连接EF交AC于点N , 连接DN、DE , 若 , , ,求AN的长.27. 如图抛物线y=ax2+2交x轴于点A(﹣2,0)、B,交y轴于点C;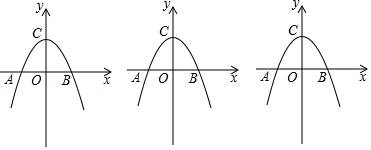 (1)、求抛物线的解析式;(2)、点P从点A出发,以1个单位/秒的速度向终点B运动,同时点Q从点C出发,以相同的速度沿y轴正方向向上运动,运动的时间为t秒,当点P到达点B时,点Q也停止运动,设△PQC的面积为S,求S与t间的函数关系式并直接写出t的取值范围;(3)、在(2)的条件下,当点P在线段OB上时,设PQ交直线AC于点G,过P作PE⊥AC于点E,求EG的长.
(1)、求抛物线的解析式;(2)、点P从点A出发,以1个单位/秒的速度向终点B运动,同时点Q从点C出发,以相同的速度沿y轴正方向向上运动,运动的时间为t秒,当点P到达点B时,点Q也停止运动,设△PQC的面积为S,求S与t间的函数关系式并直接写出t的取值范围;(3)、在(2)的条件下,当点P在线段OB上时,设PQ交直线AC于点G,过P作PE⊥AC于点E,求EG的长.