黑龙江省哈尔滨市道外区2018-2019学年九年级上学期数学期末考试试卷
试卷更新日期:2020-01-09 类型:期末考试
一、单选题
-
1. 抛物线y=(x+1)2+2的对称轴是( )A、直线x=-1 B、直线x=1 C、直线y=-1 D、直线y=12. 下列图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 3. 如图, , 是 的直径, ,若 ,则 的度数是( )
3. 如图, , 是 的直径, ,若 ,则 的度数是( )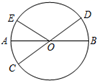 A、32° B、60° C、68° D、64°4. ⊙O的半径r=5 cm,圆心到直线l的距离OM=4 cm,在直线l上有一点P,且PM=3 cm,则点P( )A、在⊙O内 B、在⊙O上 C、在⊙O外 D、可能在⊙O上或在⊙O内5. 如图,PA切⊙O于点A,PO交⊙O于点B,若PA=8,OP=10,则⊙O的半径等于( )
A、32° B、60° C、68° D、64°4. ⊙O的半径r=5 cm,圆心到直线l的距离OM=4 cm,在直线l上有一点P,且PM=3 cm,则点P( )A、在⊙O内 B、在⊙O上 C、在⊙O外 D、可能在⊙O上或在⊙O内5. 如图,PA切⊙O于点A,PO交⊙O于点B,若PA=8,OP=10,则⊙O的半径等于( )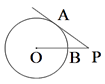 A、3 B、5 C、6 D、86. 若M(-4,y1)、N(-2,y2)、P(2,y3)三点都在反比例函数y= (k<0)的图象上,则y1、 y2、 y3的大小关系为( )A、y2>y3>y1 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y17. 下列说法错误的是( )A、必然事件发生的概率为 B、不可能事件发生的概率为 C、有机事件发生的概率大于等于 、小于等于 D、概率很小的事件不可能发生8. 若关于x的函数y=(2﹣a)x2﹣x是二次函数,则a的取值范围是( )A、a≠0 B、a≠2 C、a<2 D、a>29. 如图,分别以△ABC的三个顶点为圆心作⊙A、⊙B、⊙C,且半径都是0.5cm,则图中三个阴影部分面积之和等于( )
A、3 B、5 C、6 D、86. 若M(-4,y1)、N(-2,y2)、P(2,y3)三点都在反比例函数y= (k<0)的图象上,则y1、 y2、 y3的大小关系为( )A、y2>y3>y1 B、y2>y1>y3 C、y3>y1>y2 D、y3>y2>y17. 下列说法错误的是( )A、必然事件发生的概率为 B、不可能事件发生的概率为 C、有机事件发生的概率大于等于 、小于等于 D、概率很小的事件不可能发生8. 若关于x的函数y=(2﹣a)x2﹣x是二次函数,则a的取值范围是( )A、a≠0 B、a≠2 C、a<2 D、a>29. 如图,分别以△ABC的三个顶点为圆心作⊙A、⊙B、⊙C,且半径都是0.5cm,则图中三个阴影部分面积之和等于( ) A、 B、 C、 D、10. 如图,点E为平行四边形ABCD的边AB延长线上的一点,连接DE交BC于点F , 则下列结论一定正确的是( )
A、 B、 C、 D、10. 如图,点E为平行四边形ABCD的边AB延长线上的一点,连接DE交BC于点F , 则下列结论一定正确的是( )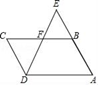 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在⊙O中,弦AB=24cm , 圆心O到弦AB的距离为5cm , 则⊙O的半径为cm .12. 二次函数y=x2+2的图象,与y轴的交点坐标为 .13. 正八边形的中心角为度.14. 在半径为12的⊙O中,150°的圆心角所对的弧长等于 .15. 扇形的圆心角为80°,弧长为4πcm,则此扇形的面积等于cm2 .16. 如图,两弦AB、CD相交于点E,且AB⊥CD,若∠B=60°,则∠A等于度.
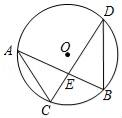 17. 点A(2,﹣4)在反比例函数y= 的图象上,则k的值等于 .18. 在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为 .
17. 点A(2,﹣4)在反比例函数y= 的图象上,则k的值等于 .18. 在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸出一个球,摸到红球的概率为 .
19. 如图,在△ABC中,已知∠C=90°,sin∠A= ,点D为边AC上一点,若∠BDC=45°,DC=6cm,则△ABC的面积等于 cm2.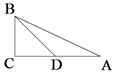 20. 如图,在四边形ABCD中,AB∥DC , AB=AD , 对角线AC、BD相交于点O , AC平分∠BAD , 过点C作CE⊥AB交AB的延长线于点E . 若AB= ,BD=2,则BE的长等于 .
20. 如图,在四边形ABCD中,AB∥DC , AB=AD , 对角线AC、BD相交于点O , AC平分∠BAD , 过点C作CE⊥AB交AB的延长线于点E . 若AB= ,BD=2,则BE的长等于 .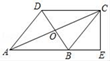
三、解答题
-
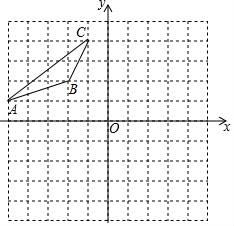
21. 先化简,再求代数式 的值,其中x=cos30°.22. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
 (1)、将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1 , 画出△A1B1C1;(2)、画出与△ABC关于原点O成中心对称的△A2B2C2 , 并直接写出点A2的坐标.23. 某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任宁老师对全
(1)、将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1 , 画出△A1B1C1;(2)、画出与△ABC关于原点O成中心对称的△A2B2C2 , 并直接写出点A2的坐标.23. 某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任宁老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
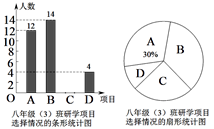 (1)、八年级(3)班学生总人数是多少,并将条形统计图补充完整;(2)、宁老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这组学生中任意挑选两名担任活动记录员,那么恰好选1名男生和1名女生担任活动记录员的概率;(3)、若学校学生总人数为2000人,根据八年级(3)班的情况,估计全校报名军事竞技的学生有多少人?24. 某数学兴趣小组的同学在一次活动中,为了测量某建筑物AB的高,他们来到另一建筑物CD上的点C处进行观察,如图所示,他们测得建筑物AB顶部A的仰角为30°,底部B的俯角为45°,已知建筑物AB、CD的距离DB为12m,求建筑物AB的高.
(1)、八年级(3)班学生总人数是多少,并将条形统计图补充完整;(2)、宁老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这组学生中任意挑选两名担任活动记录员,那么恰好选1名男生和1名女生担任活动记录员的概率;(3)、若学校学生总人数为2000人,根据八年级(3)班的情况,估计全校报名军事竞技的学生有多少人?24. 某数学兴趣小组的同学在一次活动中,为了测量某建筑物AB的高,他们来到另一建筑物CD上的点C处进行观察,如图所示,他们测得建筑物AB顶部A的仰角为30°,底部B的俯角为45°,已知建筑物AB、CD的距离DB为12m,求建筑物AB的高. 25. 某商场经调研得出某种商品每天的利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75,其图象如图所示.
25. 某商场经调研得出某种商品每天的利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx﹣75,其图象如图所示.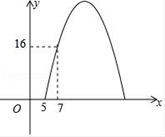 (1)、求a与b的值;(2)、销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?(参考公式:当x= 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)(3)、销售单价定在多少时,该种商品每天的销售利润为21元?结合图象,直接写出销售单价定在什么范围时,该种商品每天的销售利润不低于21元?26. 已知:△ABC是⊙O的内接三角形,且AB=BC,点D为劣弧BC上的一点,连接BD、DC.(1)、如图1,若∠BDC=120°,求证:△ABC是等边三角形;
(1)、求a与b的值;(2)、销售单价为多少元时,该种商品每天的销售利润最大?最大利润是多少元?(参考公式:当x= 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值)(3)、销售单价定在多少时,该种商品每天的销售利润为21元?结合图象,直接写出销售单价定在什么范围时,该种商品每天的销售利润不低于21元?26. 已知:△ABC是⊙O的内接三角形,且AB=BC,点D为劣弧BC上的一点,连接BD、DC.(1)、如图1,若∠BDC=120°,求证:△ABC是等边三角形;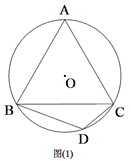 (2)、如图2,在(1)的条件下,线段CD绕点C顺时针旋转60°,得到线段CE,连接AE,求证:BD=AE;
(2)、如图2,在(1)的条件下,线段CD绕点C顺时针旋转60°,得到线段CE,连接AE,求证:BD=AE;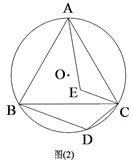 (3)、如图3,在(2)的条件下,连接OE,若⊙O的半径为 ,OE=2,求BD的长.
(3)、如图3,在(2)的条件下,连接OE,若⊙O的半径为 ,OE=2,求BD的长.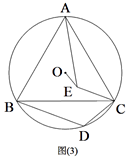 27. 如图,在平面直角坐标系xOy中,直线AB与直线y=x相交于点B , 点B的横坐标为3,点A(0,6).
27. 如图,在平面直角坐标系xOy中,直线AB与直线y=x相交于点B , 点B的横坐标为3,点A(0,6). (1)、求直线AB的解析式;(2)、动点P从原点O出发,以每秒 个单位长度的速度沿x轴正方向运动,过点P作直线y=x的垂线,垂足为C , 连接AP , AP的中点为D , 连接CD , 设CD=d , 点P运动的时间为t秒,求d与t的函数关系式;(3)、在(2)的条件下,当tan∠APC= 时,求t的值.
(1)、求直线AB的解析式;(2)、动点P从原点O出发,以每秒 个单位长度的速度沿x轴正方向运动,过点P作直线y=x的垂线,垂足为C , 连接AP , AP的中点为D , 连接CD , 设CD=d , 点P运动的时间为t秒,求d与t的函数关系式;(3)、在(2)的条件下,当tan∠APC= 时,求t的值.