黑龙江省哈尔滨市道里区2018-2019学年九年级上学期数学期末考试试卷(五四制)
试卷更新日期:2020-01-09 类型:期末考试
一、单选题
-
1. 平面直角坐标系内的点A(-2,3)关于x轴对称点的坐标是( )A、(3,-2) B、(2,-3) C、(-3,-2) D、(-2,-3)2. 下列四个图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 三个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
3. 三个大小相同的正方体搭成的几何体如图所示,其俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 关于反比例函数y= ,下列说法错误的是( )A、函数图象分别位于第一、第三象限 B、当x>0时,y随x的增大而减小 C、函数图象经过点(1,2) D、若点A(x1 , y1),B(x2 , y2)都在函数图象上,且x1<x2 , 则y1>y25. 如图,△ABC∽△ADE,且BC=2DE,则 的值为( )
4. 关于反比例函数y= ,下列说法错误的是( )A、函数图象分别位于第一、第三象限 B、当x>0时,y随x的增大而减小 C、函数图象经过点(1,2) D、若点A(x1 , y1),B(x2 , y2)都在函数图象上,且x1<x2 , 则y1>y25. 如图,△ABC∽△ADE,且BC=2DE,则 的值为( )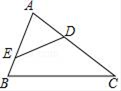 A、 B、 C、 D、6. 如图,⊙ 的直径 为10,弦 的长为8,且 ,垂足为 ,则 的长为( )
A、 B、 C、 D、6. 如图,⊙ 的直径 为10,弦 的长为8,且 ,垂足为 ,则 的长为( ) A、1 B、2 C、3 D、47. 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F,连接CD,交EF于点K,则下列说法正确的是( )
A、1 B、2 C、3 D、47. 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E作AB的平行线交BC于点F,连接CD,交EF于点K,则下列说法正确的是( ) A、 B、 C、 D、8. 如图,以点A为中心,把 逆时针旋转 ,得到 (点B,C的对应点分别为点 ),连接 ,若 ,则 的度数为( )
A、 B、 C、 D、8. 如图,以点A为中心,把 逆时针旋转 ,得到 (点B,C的对应点分别为点 ),连接 ,若 ,则 的度数为( ) A、45° B、60° C、70° D、90°9. 如图,过半径为2的 外一点P作 的两条切线PA、PB,切点分别为A,B, ,连接OP,则OP的长为
A、45° B、60° C、70° D、90°9. 如图,过半径为2的 外一点P作 的两条切线PA、PB,切点分别为A,B, ,连接OP,则OP的长为 A、 B、 C、3 D、10. 已知二次函数 图象的一部分如图所示,给出以下结论: ; 当 时,函数有最大值; 方程 的解是 , ; ,其中结论错误的个数是
A、 B、 C、3 D、10. 已知二次函数 图象的一部分如图所示,给出以下结论: ; 当 时,函数有最大值; 方程 的解是 , ; ,其中结论错误的个数是 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 函数 中,自变量 的取值范围是12. 已知点 在双曲线 上,则k的值为 .13. 将抛物线 向右平移2个单位长度,再向上平移4个单位长度,则所得抛物线的顶点坐标为14. 已知扇形的弧长为 ,它的圆心角为 ,则该扇形的半径为 .15. 一个不透明的袋子中装有4个红球,3个白球,2个黄球,这些小球除颜色不同外,其它都相同,从袋子中随机摸出1个小球,则摸出红球的概率是 .16. 若抛物线 与x轴有两个公共点,则m的取值范围是 .17. 如图,热气球的探测器显示,从热气球A看一栋大楼顶部B的俯角为30°,看这栋大楼底部C的俯角为60°,热气球A的高度为270米,则这栋大楼的高度为米.
 18. 如图,已知,在 中, , , , 是ABC的内切圆,则这个圆的半径是 .
18. 如图,已知,在 中, , , , 是ABC的内切圆,则这个圆的半径是 . 19. 已知,AB和AC是 的两条弦, ,M、N分别是AB、AC的中点,则 的度数为 .20. 如图,在菱形ABCD中, ,点E在边CD上,且 , 与 关于AE所在的直线成对称图形 以点A为中心,把 顺时针旋转 ,得到 ,连接GF,则线段GF的长为 .
19. 已知,AB和AC是 的两条弦, ,M、N分别是AB、AC的中点,则 的度数为 .20. 如图,在菱形ABCD中, ,点E在边CD上,且 , 与 关于AE所在的直线成对称图形 以点A为中心,把 顺时针旋转 ,得到 ,连接GF,则线段GF的长为 .
三、解答题
-
21. 先化简,再求代数式 ÷(x﹣3﹣ )的值,其中x=3tan45°+2cos30°.22. 如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
 (1)、在图中画出以线段AB为一边的矩形 不是正方形 ,且点C和点D均在小正方形的顶点上;(2)、在图中画出以线段AB为一腰的钝角等腰三角形ABE,点E在小正方形的顶点上,连接EC,请直接写出 的余弦值;23. 某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
(1)、在图中画出以线段AB为一边的矩形 不是正方形 ,且点C和点D均在小正方形的顶点上;(2)、在图中画出以线段AB为一腰的钝角等腰三角形ABE,点E在小正方形的顶点上,连接EC,请直接写出 的余弦值;23. 某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
 (1)、九年级接受调查的同学共有多少名,并补全条形统计图;(2)、九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.24. 已知,在 中, , ,D是AB上的一点 不与点A,B重合 ,连接CD,以点C为中心,把CD顺时针旋转 ,得到CE,连接AE.
(1)、九年级接受调查的同学共有多少名,并补全条形统计图;(2)、九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.24. 已知,在 中, , ,D是AB上的一点 不与点A,B重合 ,连接CD,以点C为中心,把CD顺时针旋转 ,得到CE,连接AE. (1)、如图1,求证: ;(2)、如图2,若 ,点G为BC上一点,连接GD并延长,与EA的延长线交于点H,且 ,连接DE与AC相交于点F,请写出图2中所有正切值为2的角.25. 某商场销售一种商品,若将50件该商品按标价打八折销售,比按原标价销售这些商品少获利200元.(1)、求该商品的标价为多少元;(2)、已知该商品的进价为每件12元,根据市场调査:若按 中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件 那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?26. 已知,四边形ABCD内接于 ,对角线AC和BD相交于点E,AC是 的直径.
(1)、如图1,求证: ;(2)、如图2,若 ,点G为BC上一点,连接GD并延长,与EA的延长线交于点H,且 ,连接DE与AC相交于点F,请写出图2中所有正切值为2的角.25. 某商场销售一种商品,若将50件该商品按标价打八折销售,比按原标价销售这些商品少获利200元.(1)、求该商品的标价为多少元;(2)、已知该商品的进价为每件12元,根据市场调査:若按 中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件 那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?26. 已知,四边形ABCD内接于 ,对角线AC和BD相交于点E,AC是 的直径. (1)、如图1,连接OB和OD,求证: ;
(1)、如图1,连接OB和OD,求证: ;
(2)、如图2,延长BA到点F,使 ,在AD上取一点G,使 ,连接FG和FC,过点G作 ,垂足为M,过点D作 ,垂足为N,求 的值;
(3)、如图3,在(2)的条件下,点H为FG的中点,连接DH交 于点K,连接AK,若 , ,求线段BC的长.27. 如图,在平面直角坐标系中,点O为坐标原点,抛物线 交x轴于点A、点 点A在点B的左边 ,交y轴于点C,直线 经过点B,交y轴于点D,且 , . (1)、求b、c的值;(2)、点 在第一象限,连接OP、BP,若 ,求点P的坐标,并直接判断点P是否在该抛物线上;(3)、在(2)的条件下,连接PD,过点P作 ,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作 ,垂足为H,若 ,求 的值.
(1)、求b、c的值;(2)、点 在第一象限,连接OP、BP,若 ,求点P的坐标,并直接判断点P是否在该抛物线上;(3)、在(2)的条件下,连接PD,过点P作 ,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作 ,垂足为H,若 ,求 的值.