黑龙江省鸡西市二中2018-2019学年七年级上学期数学期末考试试卷（五四学制)

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列各数中是无理数的有（）
$\sqrt{36}$ 、 $\frac{1}{7}$ 、0 、 $- π$ 、 $\sqrt[3]{11}$ 、3.1415、 $\sqrt{\frac{1}{5}}$ 、2.010010001…（相邻两个1之间依次增加1个0）.

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列各点中位于第四象限的点是（）

A、（3，4） B、（﹣3，4） C、（3，﹣4） D、（﹣3，﹣4）

查看试题解析
3. 已知一个正数的两个平方根分别为3a﹣1和﹣5﹣a，则这个正数的立方根是（　　）

A、﹣2 B、2 C、3 D、4

查看试题解析
4. 一商场某品牌服装统一按进价增加10%作为定价，元旦期间以9折促销．李老师在该摊位以198元的价格买了一件服装，则对于商家来说，这次生意的盈亏情况为（　　）

A、亏2元 B、不亏不赚 C、赚2元 D、亏5元

查看试题解析
5. 如图，已知AC∥BD ， ∠A＝∠C ，则下列结论不一定成立的是(　　)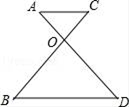

A、∠B＝∠D B、OA＝OC C、OA＝OD D、AD＝BC

查看试题解析
6. 下列各组数中，互为相反数的一组是（　　）

A、 $\sqrt{2^{2}}$ 与 $\sqrt{{(- 2)}^{2}}$ B、（ $\sqrt{2}$ ）²与 $\sqrt{2^{2}}$ C、 $\sqrt[3]{2}$ 与 $\sqrt[3]{- 2}$ D、- $\sqrt[3]{2}$ 与 $\sqrt[3]{- 2}$

查看试题解析
7. 如图，直线a、b被直线c所截，下列条件中，不能判定a∥b的是(　　)

A、∠2＝∠4 B、∠4＝∠5 C、∠1＝∠3 D、∠1+∠4＝180°

查看试题解析
8. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）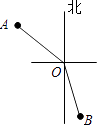

A、69° B、111° C、141° D、159°

查看试题解析
9. 若x轴上的点P到y轴的距离为2，则点P的坐标为（　　）

A、（2，0） B、（2，0）或（﹣2，0） C、（0，2） D、（0，2）或（0，﹣2）

查看试题解析
10. “某幼儿园给小朋友分苹果，若每个小朋友分3个则剩1个；若每个小朋友分4个则少2个，问苹果有多少个？”若设共有x个苹果，则列出的方程是（　　）

A、 $3 x + 1 = 4 x - 2$ B、 $3 x - 1 = 4 x + 2$ C、 $\frac{x - 1}{3} = \frac{x + 2}{4}$ D、 $\frac{x + 1}{3} = \frac{x - 2}{4}$

查看试题解析

二、填空题

11. 对于任意不相等的两个数a，b，定义一种运算※如下：a※b= $\frac{\sqrt{a + b}}{a - b}$ ，如3※2= $\frac{\sqrt{3 + 2}}{3 - 2}$ = $\sqrt{5}$ ，那么6※3= ．

查看试题解析
12. 点M（3， $-$ . 4）关于x轴的对称点的坐标是；关于y轴的对称点的坐标是．

查看试题解析
13. 如图，把一张长方形纸片沿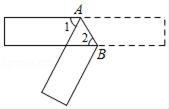 $A B$ 折叠后，若 $∠ 1 = 48 °$ ，则 $∠ 2$ 的大小为度.

查看试题解析
14. 若方程（k﹣2）x^|k^﹣^1|＝3是关于x的一元一次方程，则k＝．

查看试题解析
15. 若2a﹣4与﹣2互为相反数，则a＝．

查看试题解析
16. 若 $\sqrt[3]{25.36}$ =2.938， $\sqrt[3]{253.6}$ =6.329，则 $\sqrt[3]{25360000}$ = ．

查看试题解析
17. 如图，AB∥CD，MP∥AB，MN平分∠AMD，∠A＝40°，∠D＝30°，则∠PMN＝度．

查看试题解析
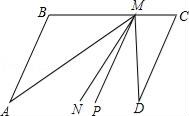18. 在平面直角坐标系中，有A、B的坐标分别为（﹣1，1）、（3，1），AB＝AC，且△ABC的面积为6，则顶点C的坐标为．

查看试题解析

三、解答题

19. 计算或解方程

(1)、﹣1⁴+（﹣5）²×（﹣ $\frac{5}{3}$ ）+|0.8﹣1|

(2)、﹣1.53×0.75+1.53× $\sqrt{{(- \frac{1}{2})}^{2}}$ + $\sqrt{\frac{25}{16}}$ ×1.53

(3)、 $\frac{{(- 1)}^{3} + | - 12 | \div [- {(- \frac{1}{2})}^{2}]}{2^{2} \times (- \frac{1}{4}) + [- 10 - 3^{2} \times (- 2)]}$

(4)、 $\frac{x + 1}{0.3} - \frac{2 x - 1}{0.7} = 1$ ．

查看试题解析
20. 如图，在平面直角坐标系中，三角形ABC的顶点A、B、C的坐标分别为（0，3）、（﹣2，1）、（﹣1，1），如果将三角形ABC先向右平移2个单位长度，再向下平移2个单位长度，会得到三角形A′B′C′，点A'、B′、C′分别为点A、B、C移动后的对应点．

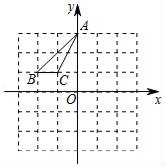(1)、请直接写出点A′、B'、C′的坐标；

(2)、请在图中画出三角形A′B′C′，并直接写出三角形A′B′C′的面积．

查看试题解析
21. 已知：如图，BE∥GF ， ∠1＝∠3，∠DBC＝70°，求∠EDB的大小．
阅读下面的解答过程，并填空(理由或数学式)

解：∵BE∥GF(已知)

∴∠2＝∠3.

∵∠1＝∠3.

∴∠1＝， .

∴DE∥ ， .

∴∠EDB+∠DBC＝180°.

∴∠EDB＝180°﹣∠DBC(等式性质)

∵∠DBC＝.(已知)

∴∠EDB＝180°﹣70°＝110°

查看试题解析
22. 已知 $\sqrt{a - 5}$ + $\sqrt{5 - a}$ =b+3

(1)、求a的值；

(2)、求a²﹣b²的平方根.

查看试题解析
23. 如图，

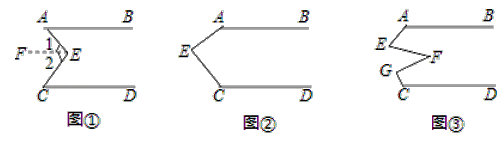(1)、（感知）如图①，AB∥CD，点E在直线AB与CD之间，连结AE、BE，试说明∠BEE+∠DCE＝∠AEC．下面给出了这道题的解题过程，请完成下面的解题过程，并填空（理由或数学式）：
解：如图①，过点E作EF∥AB

∴∠BAE＝∠1.

∵AB∥CD.

∴CD∥EF.

∴∠2＝∠DCE

∴∠BAE+∠DCE＝∠1+∠2.

∴∠BAE+∠DCE＝∠AEC

(2)、（探究）当点E在如图②的位置时，其他条件不变，试说明∠AEC+∠FGC+∠DCE＝360°；

(3)、（应用）点E、F、G在直线AB与CD之间，连结AE、EF、FG和CG，其他条件不变，如图③．若∠EFG＝36°，则∠BAE+∠AEF+∠FGC+∠DCG＝°．

查看试题解析
24. 近期，重庆商品住宅市场房屋销售出现销售量和销售价齐涨态势，数据显示，2016年12月，甲、乙房地产公司的销售面积一共17000平方米，乙房地产公司的单价是甲房地产公司单价的 $\frac{9}{8}$ ．甲房地产公司单价为每平方米0.8万元，两家销售的总金额为14430万元．

(1)、求2016年12月，甲、乙房地产公司各销售了多少平方米．

(2)、根据市场需求，甲、乙房地产公司决定调整2017年1月份的房价，甲房地产公司每平方米的售价上涨a%，销售量预计比12月减少200平方米：乙房地产公司决定以降价促销的方式应对当前的形势，每平方米的售价下调 $\frac{1}{3}$ a%，销售面积预计将比12月增加700平方米，预计1月份两家的总销售额恰好为15310万元，求a的值．

查看试题解析
25. 如图，在平面直角坐标系中，点M的坐标为（2，8），点N的坐标为（2，6），将线段MN向右平移4个单位长度得到线段PQ（点P和点Q分别是点M和点N的对应点），连接MP、NQ，点K是线段MP的中点．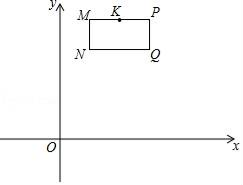

(1)、求点K的坐标；

(2)、若长方形PMNQ以每秒1个单位长度的速度向正下方运动，（点A、B、C、D、E分别是点M、N、Q、P、K的对应点），当BC与x轴重合时停止运动，连接OA、OE，设运动时间为t秒，请用含t的式子表示三角形OAE的面积S（不要求写出t的取值范围）；

(3)、在（2）的条件下，连接OB、OD，问是否存在某一时刻t，使三角形OBD的面积等于三角形OAE的面积？若存在，请求出t值；若不存在，请说明理由．

查看试题解析