黑龙江省哈尔滨市尚志市2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列一组数：﹣8，0，﹣3² ， ﹣（﹣5.7），其中负数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列比较大小结果正确的是（）

A、﹣3＜﹣4 B、﹣（﹣2）＜|﹣2| C、 $- \frac{1}{2} > - \frac{1}{3}$ D、 $| - \frac{1}{8} | > - \frac{1}{7}$

查看试题解析
3.
由4个相同的小立方体搭成的几何体如图所示，则它的主视图是（　　）

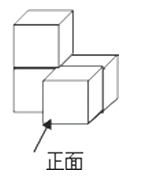A、 B、 C、 D、

查看试题解析
4. 已知数轴上的三点A、B、C，分别表示有理数a、1、﹣1，那么|a+1|表示为（）

A、A、B两点间的距离 B、A、C两点间的距离 C、A、B两点到原点的距离之和 D、A、C两点到原点的距离之和

查看试题解析
5. 计算：（-12）+（+ $\frac{6}{5}$ ）+（-8）+（- $\frac{7}{10}$ ）+（- $\frac{1}{2}$ ）=（）

A、-19 B、-18 C、-20 D、-17

查看试题解析
6. 如图，将一副三角尺按不同的位置摆放，下列摆放方式中 $∠ a$ 与 $∠ β$ 互余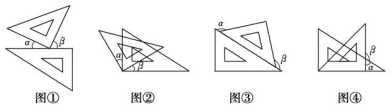的是（）

A、图① B、图② C、图③ D、图④

查看试题解析
7. 如图，将边长为3a的正方形沿虚线剪成两块正方形和两块长方形．若拿掉边长2b的小正方形后，再将剩下的三块拼成一块矩形，则这块矩形较长的边长为（）

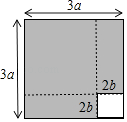A、3a+2b B、3a+4b C、6a+2b D、6a+4b

查看试题解析
8. 下列说法正确的是（　　）

A、一点确定一条直线 B、两条射线组成的图形叫角 C、两点之间线段最短 D、若AB=BC，则B为AC的中点

查看试题解析
9. 小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是： $2 y - \frac{1}{2} = \frac{1}{2} y -$ ，怎么呢？小明想了一想，便翻看书后答案，此方程的解是 $y = - \frac{5}{3}$ ，很快补好了这个常数，并迅速地完成了作业，同学们，你们能补出这个常数吗？它应是（）

A、1 B、2 C、3 D、4

查看试题解析
10. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）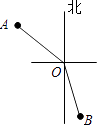

A、69° B、111° C、141° D、159°

查看试题解析

二、填空题

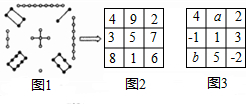
11. 今年“五一”节日期间，我市四个旅游景区共接待游客约303000多人次，这个数据用科学记数法可记为．

查看试题解析
12. （阅读材料）“九宫图”源于我国古代夏禹时期的“洛书” $($ 图1所示 $)$ ，是世界上最早的矩阵，又称“幻方”，用今天的数学符号翻译出来，“洛书”就是一个三阶“幻方” $($ 图2所示 $)$ ．
（规律总结）观察图1、图2，根据“九宫图”中各数字之间的关系，我们可以总结出“幻方”需要满足的条件是；若图3，是一个“幻方”，则 $a =$ ．

查看试题解析
13. 有一串式子：﹣x，2x² ， ﹣3x³ ， 4x⁴ ， …，﹣19x¹⁹ ， 20x²⁰ ， …写出第 2013 个式子，写出第 n 个．

查看试题解析
14. 已知|x﹣2|+|y+2|=0，则x+y= ．

查看试题解析
15. 若∠α=60°25′，则∠α的补角大小为．

查看试题解析
16. 如果 $\frac{7}{5}$ x³ⁿy^m⁺⁴与﹣3x⁶y²ⁿ是同类项，那么mn的值为．

查看试题解析
17. 有甲、乙两桶油，从甲桶到出 $\frac{1}{4}$ 到乙桶后，乙桶比甲桶还少6升，乙桶原有油30升，设甲有油x升，可列方程为．

查看试题解析
18. 图中有条线段．

查看试题解析
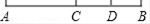19. 如图，点C是线段AB上一点，AC＜CB，M、N分别是AB和CB的中点，AC=8，NB=5，则线段MN=.

查看试题解析
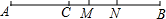20. 一个由16个完全相同的小立方块搭成的几何体，其最下面一层摆放了9个小立方块，它的主视图和左视图如图所示，那么这个几何体的搭法共有种．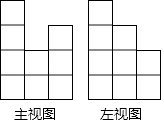

查看试题解析

三、解答题

21. 计算：

(1)、 $(\frac{1}{6} - \frac{3}{4} + \frac{1}{12}) \times (- 48)$ ；

(2)、﹣1¹⁰﹣8÷（﹣2）+4×|﹣5|.

查看试题解析
22. 解下列方程：

(1)、 $\frac{1}{2}$ a﹣6= $\frac{3}{4}$ a+1；

(2)、3x+ $\frac{x - 1}{2}$ =3﹣ $\frac{2 x + 1}{3}$ ．

查看试题解析
23. 先化简，再求值：（2x²﹣2y²）﹣3（x²y²+x²）+3（x²y²+y²），其中x＝﹣1，y＝2.

查看试题解析
24. 如图，已知A，B，C，D是平面内四个点，请根据下列要求在所给图中作图．

(1)、画直线AB，

(2)、画射线AC，

(3)、画线段AD，

(4)、画∠DBC，

(5)、作直线BD与射线AC相交于点O．

查看试题解析
25. 列方程解应用题:
某社区超市第一次用 $6000$ 元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的一半多 $15$ 件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价－进价）

甲

乙

进价(元/件)

    $22$

    $30$

售价(元/件)

    $29$

    $40$

(1)、该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?

(2)、该超市第二次以第一次的进价又购进甲、乙两种商品.其中购进甲种商品的件数不变，购进的乙种商品的件数是第一次购进乙种商品件数的 $3$ 倍；甲商品按原价销售，乙商品打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多 $180$ 元，求第二次乙种商品是按原价打几折销售？

查看试题解析
26. 如图，OM是∠AOC的平分线，ON是∠BOC的平分线．

(1)、如图1，当∠AOB是直角，∠BOC=60°时，∠MON的度数是多少？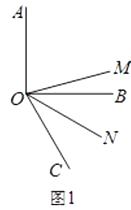

(2)、如图2，当∠AOB=α，∠BOC=60°时，猜想∠MON与α的数量关系；

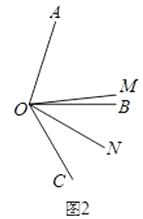(3)、如图3，当∠AOB=α，∠BOC=β时，猜想∠MON与α、β有数量关系吗？如果有，指出结论并说明理由．

查看试题解析
27. 如图数轴上A、B、C三点对应的数分别是a、b、7，满足OA=3，BC=1，P为数轴上一动点，点P从A出发，沿数轴正方向以每秒1.5个单位长度的速度匀速运动，点Q从点C出发在射线CA上向点A匀速运动，且P、Q两点同时出发．

(1)、求a、b的值

(2)、当P运动到线段OB的中点时，点Q运动的位置恰好是线段AB靠近点B的三等分点，求点Q的运动速度

(3)、当P、Q两点间的距离是6个单位长度时，求OP的长．

查看试题解析

	甲	乙
进价(元/件)	$22$	$30$
售价(元/件)	$29$	$40$