黑龙江省哈尔滨市南岗区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元一次方程的是（　　）

A、x²=25 B、x﹣5=6 C、 $\frac{1}{3}$ x﹣y=6 D、 $\frac{1}{x}$ =2

查看试题解析
2. 在平面直角坐标系中，点（﹣6，2）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列实数中，不是无理数的是（　　）

A、 $\frac{2}{11}$ B、﹣ $\sqrt{5}$ C、2π（π表示圆周率） D、2 $\sqrt{3}$

查看试题解析
4. 在下列变形中，运用等式的性质变形正确的是（　　）

A、若a=b，则a+c=b﹣c B、若a=b，则 $\frac{a}{2}$ = $\frac{b}{4}$ C、若ac=bc，则a=b D、若a=b，则a+b=2b

查看试题解析
5. 已知四条直线a，b，c，d在同一平面内，a⊥b，b⊥c，c⊥d，则下列式子成立的是（　　）

A、a⊥c B、b⊥d C、a⊥d D、a∥d

查看试题解析
6. 已知x的5倍与2的和等于x的3倍与4的差，则x的值为（）

A、﹣3 B、﹣1 C、1 D、3

查看试题解析
7. 如图，直线AB∥CD，AF交CD于点E，∠CEF=140°，则∠A等于（）

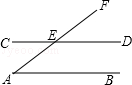A、 35° B、 40° C、 45° D、 50°

查看试题解析
8. 三角形A′B′C′是由三角形ABC平移得到的，点A（－1，4）的对应点为A′（1，7），点B（1，1）的对应点为B′（3，4），则点C（－4，－1）的对应点C′的坐标为（）

A、（－6，2） B、（－6，－4） C、（－2，2） D、（－2，－4）

查看试题解析
9. 把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本．若设这个班有x名学生，则依题意所列方程正确的是（）

A、3x－20＝4x－25 B、3x＋20＝4x＋25 C、3x－20＝4x＋25 D、3x＋20＝4x－25

查看试题解析
10. 如图，∠BCD＝90°，AB∥DE，则α与β一定满足的等式是（）

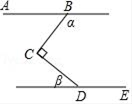A、α+β＝180° B、α+β＝90° C、β＝3α D、α﹣β＝90°

查看试题解析

二、填空题

11. 已知x=1是关于x的方程4x﹣m=2的解，则m的值为．

查看试题解析
12. 在平面直角坐标系中，点A（2t﹣1，3t+2）在y轴上，则t的值为．

查看试题解析
13. 列等式表示：比b的一半小7的数等于a与b的和．

查看试题解析
14. 把命题“邻补角互补”改写成“如果…，那么…”的形式．

查看试题解析
15. 已知(x﹣1)³=64，则x的值为．

查看试题解析
16. 在梯形面积公式s= $\frac{1}{2}$ （a+b）h中，已知s=60，b=4，h=12，则a= ．

查看试题解析
17. 如图，直线AB和CD相交于点O，OE⊥AB，∠AOD=125°，则∠COE的度数是度．

查看试题解析
18. 在一张普通的月历中，相邻三行里同一列的三个日期数之和为39，则这三个日期数分别为．

查看试题解析
19. 下列四个命题：
①互为邻补角的两个角的平分线互相垂直；

②经过一点，有且只有一条直线与已知直线平行；

③坐标平面内的点与有序实数对是一一对应的；

④实数a是实数a²的算术平方根．

其中正确命题的序号为．

查看试题解析
20. 在平面直角坐标系中，对于不在坐标轴上的任意一点P（x，y），我们把点P′（ $\frac{1}{x}$ ， $\frac{1}{y}$ ）称为点P的“倒影点”．若点A在x轴的下方，且点A的“倒影点”A′与点A是同一个点，则点A的坐标为．

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt[3]{- 8} - \sqrt{81}$

(2)、 $| \sqrt{2} - \sqrt{3} | + 2 \sqrt{2}$

查看试题解析
22. 解下列方程：

(1)、3x+5=4x+1

(2)、 $\frac{3 y - 1}{4} - 1 = \frac{5 y - 7}{6}$ .

查看试题解析
23. 完成下面的证明：如图，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，连接DE，DF，DE∥AB，∠BFD＝∠CED，连接BE交DF于点G，求证：∠EGF+∠AEG＝180°．
证明：∵DE∥AB（已知），

∴∠A＝∠CED

又∵∠BFD＝∠CED（已知），

∴∠A＝∠BFD

∴DF∥AE

∴∠EGF+∠AEG＝180°

查看试题解析
24. 如图所示的圆柱形容器的容积为81升，它的底面直径是高的2倍．（π取3）

(1)、这个圆柱形容器的底面直径为多少分米？

(2)、若这个圆柱形容器的两个底面与侧面都是用铁皮制作的，则制作这个圆柱形容器需要铁皮多少平方分米？（不计损耗）

查看试题解析
25. 在平面直角坐标系中，点O为坐标原点，我们把横、纵坐标都为整数的点称为整点，记定点都是整点的三角形为整点三角形．如图，已知整点O（0，0），A（2，4），请在所给网格区域（含边界）上按要求画图．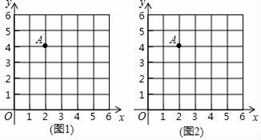

(1)、在图1中画一个整点三角形OAB，其中点B在第一象限，且点B的横、纵坐标之和等于点A的横坐标；

(2)、在图2中画一个整点三角形OAC，其中点C的坐标为（3t，t），且点C的横、纵坐标之和是点A的纵坐标的2倍．请直接写出△OAC的面积．

查看试题解析
26. 某校七年级10个班师生举行文艺汇演，每班2个节目，有歌唱与舞蹈两类节目，七年级统计后发现歌唱类节目比跳舞类节目数的2倍少4个．

(1)、七年级师生表演的歌唱与舞蹈类节目数各有多少个？

(2)、该校七、八年级师生有小品节目参与，在歌唱、舞蹈、小品三类节目中，每个节目的演出平均用时分别是5分钟、6分钟、8分钟，预计所有演出节目交接用时共花15分钟．若从开始到结束共用2小时35分钟，问参与的小品类节目有多少个？

查看试题解析
27. 已知：点A在射线CE上，∠C＝∠D．

(1)、如图1，若AC∥BD，求证：AD∥BC；

(2)、如图2，若∠BAC＝∠BAD，BD⊥BC，请探究∠DAE与∠C的数量关系，写出你的探究结论，并加以证明；

(3)、如图3，在（2）的条件下，过点D作DF∥BC交射线于点F，当∠DFE＝8∠DAE时，求∠BAD的度数．

查看试题解析