黑龙江省哈尔滨市道外区2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元一次方程的是（）

A、 $\frac{1}{x} = 2$ B、 $x^{2} - 4 x = 3$ C、 $\frac{1}{2} x - 1 = 3 x$ D、 $2 x - 5 y = 6$

查看试题解析
2. 点 $(- 1, 8)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 正数5的算术平方根是（）

A、 $\pm \sqrt{5}$ B、 $\pm \frac{5}{2}$ C、 $\sqrt{5}$ D、 $- \sqrt{5}$

查看试题解析
4. 在实数 $- \frac{1}{3}, 0, \sqrt{3}, 3.14, \sqrt{4}$ 中，无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 如图，两直线被第三直线所截，下列说法中错误的是（）

A、 $∠ 1$ 和 $∠ 2$ 是对顶角 B、 $∠ 2$ 和 $∠ 3$ 是内错角 C、 $∠ 2$ 和 $∠ 4$ 是同位角 D、 $∠ 1$ 和 $∠ 4$ 是同旁内角

查看试题解析
6. 下列所给的方程变形中，正确的是（）

A、把方程 $3 x - 2 = 2 x + 1$ 移项得 $3 x - 2 x = - 1 + 2$ B、把方程 $3 - x = 2 - 5 (x - 1)$ 去括号得 $3 - x = 2 - 5 x - 1$ C、若 $a x = a y$ ，则 $x = y$ D、方程 $\frac{x}{2} - \frac{x}{3} = 1$ 去分母得 $3 x - 2 x = 6$

查看试题解析
7. 若方程 $2 x + a - 4 = 0$ 的解是 $x = - 2$ ，则 $a$ 的值为（）

A、8 B、0 C、2 D、-8

查看试题解析
8. 在坐标平面中，把点 $A (- 2, 1)$ 向右平移3个单位长度，再向上平移2个单位长度得到对应点 $B$ ，则对应点 $B$ 的坐标是（）

A、（3，1） B、（-1，-3） C、（1，3） D、（-3，-1）

查看试题解析
9. 现有鸡、兔同笼，已知鸡与兔头数之和为100，鸡与兔之脚数之和为360，设鸡有x只，所列方程是（）

A、 $2 x + 4 (100 - x) = 360$ B、 $2 x + 4 \times 100 = 360$ C、 $4 x + 2 (100 - x) = 360$ D、 $4 x + 2 \times 100 = 360$

查看试题解析
10. 有下列命题：①无理数是无限不循环小数；②64的平方根是8；③过一点有且只有一条直线与这条直线平行；④两条直线被第三条直线所截，同位角相等，其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. m的相反数是．

查看试题解析
12. 计算： $\sqrt{2} + (\sqrt{3} - \sqrt{2}) =$ ．

查看试题解析
13. 比较大小： $\sqrt{2}$ $\frac{3}{2}$ （用“＞”或“＜”填空）．

查看试题解析
14. 若 $x^{3} = 8$ ，则 $x$ 的值为．

查看试题解析
15. 坐标系中，点P（－3,4）到y轴的距离是.

查看试题解析
16. 如图，要把河中的水引到水池A中，应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短，这样做的理由是．

查看试题解析
17. 如图，AB∥CD，∠B=26°，∠D=39°，则∠BED的度数为．

查看试题解析
18. 已知两个角的两边分别互相平行，如果其中一个角的度数是 $70^{0}$ ，那么另一个角的度数为．

查看试题解析
19. 一件工作，甲单独做10小时完成，乙单独做15小时完成，现在先由甲单独做5小时，剩下的部分由甲、乙合作，剩下的部分需要小时完成.

查看试题解析
20. 如图，把长方形纸片 $A B C D$ 沿折痕 $E F$ 折叠，使点 $B$ 与点 $D$ 重合，点 $A$ 落在点 $G$ 处，若 $∠ B E F = 65^{0}$ ，则 $∠ D F G$ 的度数为．

查看试题解析

三、解答题

21. 完成下面的证明．
已知，如图所示，BCE，AFE是直线，

AB∥CD，∠1=∠2，∠3=∠4．

求证：AD∥BE

证明：∵AB∥CD（已知）

∴∠4=∠ ， .

∵∠3=∠4（已知）

∴∠3=∠ ， .

∵∠1=∠2（已知）

∴∠1+∠CAF=∠2+∠CAF

即：∠=∠ ．

∴∠3=∠ .

∴AD∥BE.

查看试题解析
22. 解方程:

(1)、 $3 (x + 1) - x = 13 - 2 (x - 1)$ ；

(2)、 $\frac{y + 1}{2} - 1 = 2 + \frac{2 - y}{4}$ .

查看试题解析
23. 如图，△ABC的顶点都在方格纸的格点上，将△ABC向右平移4格，再向下平移3格，其中每个格子的边长为1个单位长度．

(1)、请在图中画出平移后的△A′B′C′；

(2)、求△ABC的面积．

查看试题解析
24. 已知-3是 $2 a - 1$ 的平方根， $3 a + 2 b + 4$ 的立方根是3，求 $a + b$ 的平方根.

查看试题解析
25. 某中学开学初在商场购进 $A, B$ 两种品牌的足球，一个 $A$ 品牌的足球50元，一个 $B$ 品牌的足球80元，且购买 $A$ 品牌足球的数量是 $B$ 品牌足球数量的2倍，已知购买 $A$ 品牌足球比购买 $B$ 品牌足球多花500元.

(1)、求购买 $A$ 品牌足球和购买 $B$ 品牌足球分别花了多少元？

(2)、该中学为了响应习总书记“足球进校园”的号召，决定再次购进 $A, B$ 两种品牌足球共50个，恰逢商场对两种品牌足球的售价进行调整， $A$ 品牌足球售价比第一次购买时提高了8%， $B$ 品牌足球按第一次购买时售价的9折出售，如果这所中学此次购买 $A, B$ 两种品牌足球的总费用为3240元，那么该中学此次购买了多少个 $B$ 品牌足球？

查看试题解析
26. 如图，∠ACE=∠AEC．

(1)、若CE平分∠ACD，求证：AB∥CD．

(2)、若AB∥CD，求证：CE平分∠ACD．请在（1）、（2）中选择一个进行证明．

查看试题解析
27. 如图，平面直角坐标系中，ABCD为长方形，其中点A、C坐标分别为（﹣8，4）、（2，﹣8），且AD∥x轴，交y轴于M点，AB交x轴于N．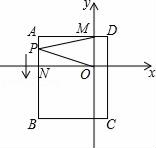

(1)、求B、D两点坐标和长方形ABCD的面积；

(2)、一动点P从A出发（不与A点重合），以 $\frac{1}{2}$ 个单位/秒的速度沿AB向B点运动，在P点运动过程中，连接MP、OP，请直接写出∠AMP、∠MPO、∠PON之间的数量关系；

(3)、是否存在某一时刻t，使三角形AMP的面积等于长方形面积的 $\frac{1}{3}$ ？若存在，求t的值并求此时点P的坐标；若不存在请说明理由．

查看试题解析