黑龙江哈尔滨市香坊区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-09 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点(-3,4)所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列方程是一元一次方程的是( )A、2x﹣y=0 B、x2﹣x=1 C、xy﹣3=5 D、x+1=23. 16的算术平方根是( )A、4 B、±4 C、8 D、±84. 已知等式 ,下列变形不一定成立的是( )A、 B、 C、 D、5. 在 , , , , 中,无理数有( )个.A、 B、 C、 D、6. 如图,点 、 分别为三角形 边 、 上一点,作射线 ,则下列说法错误的是( )
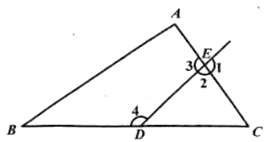 A、 与 是对顶角; B、 与 是同位角 C、 与 是同旁内角; D、 与 是内错角.7. 如图,两只蚂蚁以相同的速度沿甲、乙两条不同的路线,同时从 出发爬向终点 ,则( )
A、 与 是对顶角; B、 与 是同位角 C、 与 是同旁内角; D、 与 是内错角.7. 如图,两只蚂蚁以相同的速度沿甲、乙两条不同的路线,同时从 出发爬向终点 ,则( )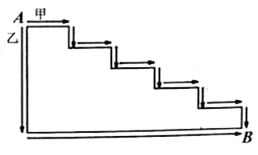 A、按甲路线走的蚂蚁先到终点 B、按乙路线走的蚂蚁先到终点 C、两只蚂蚁同时到终点 D、无法确定8. 用 张白铁皮做罐头盒,每张白铁皮可制盒身 个或盒底 个,一个盒身与两个盒底配成一套罐头盒.设把 张白铁皮制盒身,则可列方程为( ).A、 B、 C、 D、9. 如图,在数轴上表示 , 的对应点分别为 , ,点 是 的中点,则点 表示的数是( )
A、按甲路线走的蚂蚁先到终点 B、按乙路线走的蚂蚁先到终点 C、两只蚂蚁同时到终点 D、无法确定8. 用 张白铁皮做罐头盒,每张白铁皮可制盒身 个或盒底 个,一个盒身与两个盒底配成一套罐头盒.设把 张白铁皮制盒身,则可列方程为( ).A、 B、 C、 D、9. 如图,在数轴上表示 , 的对应点分别为 , ,点 是 的中点,则点 表示的数是( )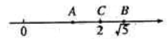 A、 B、 C、 D、10. 在下列命题中:①过一点有且只有一条直线与已知直线平行;②平方根与立方根相等的数有 和 ;③在同一平面内,如果 , ,则 ;④直线 外一点 与直线 上各点连接而成的所有线段中,最短线段的长是 ,则点 到直线 的距离是 ;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )A、 个 B、 个 C、 个 D、 个
A、 B、 C、 D、10. 在下列命题中:①过一点有且只有一条直线与已知直线平行;②平方根与立方根相等的数有 和 ;③在同一平面内,如果 , ,则 ;④直线 外一点 与直线 上各点连接而成的所有线段中,最短线段的长是 ,则点 到直线 的距离是 ;⑤无理数包括正无理数、零和负无理数.其中真命题的个数是( )A、 个 B、 个 C、 个 D、 个二、填空题
-
11. 的相反数是.12. 若关于 的方程 的解是 ,则a的值等于.13. 比较大小: .14. 如图,平行线 、 被直线 所截, ,则 =°
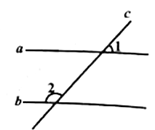 15. 一个数的立方根是 ,则这个数的算术平方根是.16. 有一列数,按一定规律排成: , , , , , , ,其中某三个相邻数的和是 ,则这三个相邻数中最小的数为.17. 如图,直线 、 相交于点 , ,垂足为 ,若射线 在 的内部, , ,则 =°.
15. 一个数的立方根是 ,则这个数的算术平方根是.16. 有一列数,按一定规律排成: , , , , , , ,其中某三个相邻数的和是 ,则这三个相邻数中最小的数为.17. 如图,直线 、 相交于点 , ,垂足为 ,若射线 在 的内部, , ,则 =°.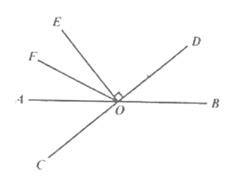 18. 如图,在平面直角坐标系中, 为坐标原点,点 和点 是坐标轴上两点,点 为坐标轴上一点,若三角形 的面积为 ,则 点坐标为.
18. 如图,在平面直角坐标系中, 为坐标原点,点 和点 是坐标轴上两点,点 为坐标轴上一点,若三角形 的面积为 ,则 点坐标为.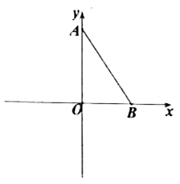 19. 如图,在三角形 中, ,垂足为点 ,直线 过点 ,且 ,点 为线段 上一点,连接 ,∠BCG与∠BCE的角平分线CM、CN分别交 于点M、N,若 ,则 =°.
19. 如图,在三角形 中, ,垂足为点 ,直线 过点 ,且 ,点 为线段 上一点,连接 ,∠BCG与∠BCE的角平分线CM、CN分别交 于点M、N,若 ,则 =°.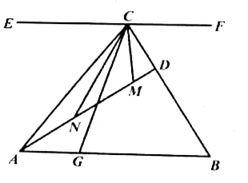
三、解答题
-
20. 计算(1)、(2)、21. 解方程(1)、(2)、22. 如图,在平面直角坐标系中,三角形 的顶点 、 、 的坐标分别为 、 、 .如果将三角形 先向右平移 个单位长度,再向下平移 个单位长度,会得到三角形 ,点 、 、 分别为点 、 、 移动后的对应点.
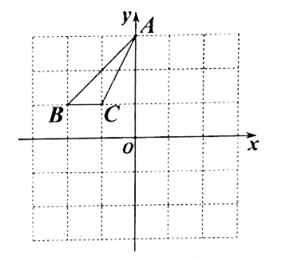 (1)、请直接写出点 、 、 的坐标.(2)、请在图中画出三角形 ,并直接写出三角形 的面积.23. 如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF.
(1)、请直接写出点 、 、 的坐标.(2)、请在图中画出三角形 ,并直接写出三角形 的面积.23. 如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF. (1)、求证:∠DAF=∠F;(2)、在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.24. 寒假将近,某学校将组织七年级部分同学去亚布力参加“冰雪冬令营”.学校提前给所去学生预定房间,如果在所预定的房间里每间住 人,则有 人无法安排;每间住 人,则空出 张床.(1)、本次参加“冰雪冬令营”的学生总数为多少人?(2)、冬令营结束时,学校准备给这些同学每人送一个售价为 元的 或 种纪念品,但实际购买时发现, 、 两种商品的售价都有变动, 种商品打八折出售, 种商品的价钱比原售价提高了 ,若实际购买 种商品费用比购买 种商品费用的 倍多 元,那么此次活动中学校购买 种商品多少个?25.
(1)、求证:∠DAF=∠F;(2)、在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.24. 寒假将近,某学校将组织七年级部分同学去亚布力参加“冰雪冬令营”.学校提前给所去学生预定房间,如果在所预定的房间里每间住 人,则有 人无法安排;每间住 人,则空出 张床.(1)、本次参加“冰雪冬令营”的学生总数为多少人?(2)、冬令营结束时,学校准备给这些同学每人送一个售价为 元的 或 种纪念品,但实际购买时发现, 、 两种商品的售价都有变动, 种商品打八折出售, 种商品的价钱比原售价提高了 ,若实际购买 种商品费用比购买 种商品费用的 倍多 元,那么此次活动中学校购买 种商品多少个?25.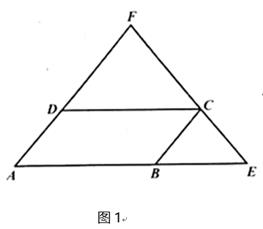
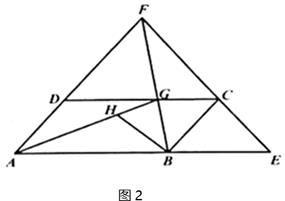
如图1,在四边形ABCD中,点E为AB延长线上一点,连接 并延长交AD延长线于点 , , .
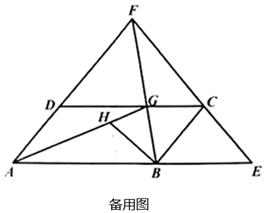
(1)、求证: ;(2)、如图2,连接 交 于点 ,连接 ,若 为 的角平分线, 为 的角平分线,过点 作 交 于点 ,求证: ;(3)、在(2)的条件下,若 , ,求 的度数.26. 如图,在平面直角坐标中,点 的坐标为 ,点 的坐标为 ,将线段 向右平移 个单位长度得到线段 (点 和点 分别是点 和点 的对应点),连接 、 ,点 是线段 的中点.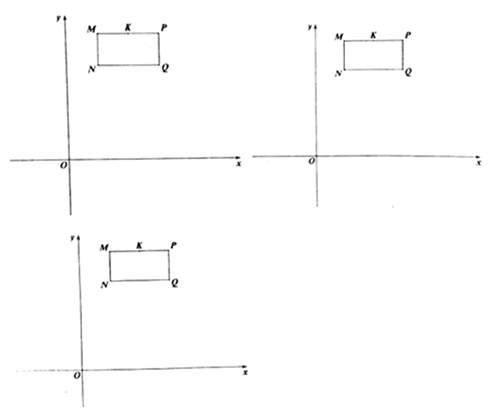 (1)、求点 的坐标;(2)、若长方形 以每秒 个单位长度的速度向正下方运动,(点 、 、 、 、 分别是点 、 、 、 、 的对应点),当 与 轴重合时停止运动,连接 、 ,设运动时间为 妙,请用含 的式子表示三角形 的面积 (不要求写出 的取值范围);(3)、在(2)的条件下,连接 、 ,问是否存在某一时刻 ,使三角形 的面积等于三角形 的面积?若存在,请求出 值;若不存在,请说明理由.
(1)、求点 的坐标;(2)、若长方形 以每秒 个单位长度的速度向正下方运动,(点 、 、 、 、 分别是点 、 、 、 、 的对应点),当 与 轴重合时停止运动,连接 、 ,设运动时间为 妙,请用含 的式子表示三角形 的面积 (不要求写出 的取值范围);(3)、在(2)的条件下,连接 、 ,问是否存在某一时刻 ,使三角形 的面积等于三角形 的面积?若存在,请求出 值;若不存在,请说明理由.