黑龙江省伊春市嘉荫县2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各运算中，计算正确的是（）

A、2a•3a＝6a B、(3a²)³＝27a⁶ C、a⁴÷a²＝2a D、(a+b)²＝a²+ab+b²

查看试题解析
2. 下列图形不是轴对称图形的是（　）

A、 B、 C、 D、

查看试题解析
3. 下列说法正确的是（　　）

A、圆有无数条对称轴，对称轴是直径所在的直线 B、正方形有两条对称轴 C、两个图形全等，那么这两个图形必成轴对称 D、等腰三角形的对称轴是高所在的直线

查看试题解析
4. 如图，D是BC的中点，E是AC的中点，△ADE的面积为2，则△ABC的面积为（　　）

A、4 B、8 C、10 D、12

查看试题解析
5. 如图所示，点A、B分别是∠NOP、∠MOP平分线上的点，AB⊥OP于点E ， BC⊥MN于点C ， AD⊥MN于点D ，下列结论错误的是(　　)

A、AD＋BC＝AB B、与∠CBO互余的角有两个 C、∠AOB＝90° D、点O是CD的中点

查看试题解析
6. 如图，在△ABC中，∠C＝70º，沿图中虚线截去∠C，则∠1＋∠2＝（）

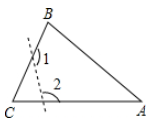A、360º B、250º C、180º D、140º

查看试题解析
7. 已知 $\frac{1}{m} + \frac{1}{n} = \frac{1}{m + n}$ ，则 $\frac{n}{m} + \frac{m}{n}$ 等于（）

A、1 B、 $- 1$ C、0 D、2

查看试题解析
8. 已知关于x的方程 $\frac{2 x + a}{x - 1}$ ＝1的解是非负数，则a的取值范围是（　　）

A、a≥﹣1 B、a≥﹣1且a≠0 C、a≤﹣1 D、a≤﹣1且a≠﹣2

查看试题解析
9. 从甲地到乙地有两条公路，一条是全长450公里的普通公路，一条是全长330公里的高速公路，某客车在高速公路上行驶的平均速度比在普通公路上快35公里/小时，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半．如果设该客车由高速公路从甲地到乙地所需时间为x小时，那么x满足的分式方程是（）

A、 $\frac{450}{x}$ = $\frac{330}{x + 35}$ ×2 B、 $\frac{450}{x}$ = $\frac{330}{2 x}$ ﹣35 C、 $\frac{450}{x}$ ﹣ $\frac{330}{2 x}$ =35 D、 $\frac{330}{x}$ ﹣ $\frac{450}{2 x}$ =35

查看试题解析
10. 如图，BN为∠MBC的平分线，P为BN上一点，且PD⊥BC于点D ， ∠APC+∠ABC＝180°，给出下列结论：①∠MAP＝∠BCP；②PA＝PC；③AB+BC＝2BD；④四边形BAPC的面积是△PBD面积的2倍，其中结论正确的个数有（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 甲型H7N9流感病毒的直径大约为0.00000008米，用科学记数法表示为米．

查看试题解析
12. 已知式子 $\frac{3}{x - 2}$ +（x﹣3）⁰有意义，则x的取值范围是．

查看试题解析
13. 如图，AB＝AC ，点D在AB上，点E在AC上，DC ， EB交于点F ，请添加一个条件．使△ADC≌△AEB（填一个即可）

查看试题解析
14. 工人师傅在安装木制门框时，为防止变形常常像图中所示，钉上两条斜拉的木条，这样做的原理是根据三角形的性．

查看试题解析
15. 若 $a + b = 2$ ， $a b = - 3$ ，则代数式 $a^{3} b + 2 a^{2} b^{2} + a b^{3}$ 的值为．

查看试题解析
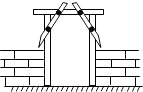16. 已知△ABC是等腰三角形，它的周长为20cm ，一条边长6cm ，那么腰长是．

查看试题解析
17. 如图，△ABC的周长为12，OB、OC分别平分∠ABC和∠ACB，过点O作OD⊥BC于点D，OD=3，则△ABC的面积为.

查看试题解析
18. 当 $m =$ 时，关于 $x$ 的分式方程 $\frac{2}{x - 2} + \frac{m x}{x^{2} - 4} = \frac{3}{x + 2}$ 无解

查看试题解析
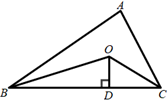19. 在 △ABC 中， AB=AC， AB 的垂直平分线与 AC 所在的直线相交所得的锐角为50 ° ，则底角 $B$ 的大小为

查看试题解析
20. 如图所示，已知：点A（0，0），B（ $\sqrt{3}$ ，0），C（0，1）在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA₁B₁ ，第2个△B₁A₂B₂ ，第3个△B₂A₃B₃ ， …，则第n个等边三角形的边长等于．

查看试题解析

三、解答题

21. 先化简，再求值： $(\frac{x - 1}{x} - \frac{x - 2}{x + 1}) \div \frac{2 x^{2} - x}{x^{2} + 2 x + 1}$ ，其中x＝ $\sqrt{3}$ ．

查看试题解析
22. 在如图所示的直角坐标系中，每个小方格都是边长为1的正方形，△ABC的顶点均在格点上，点A的坐标是（﹣3，﹣1）．

(1)、画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点B₁和点C₁的坐标；

(2)、求出△ABC的面积．

查看试题解析
23. 如图CE＝CB，CD＝CA，∠DCA＝∠ECB，求证：DE＝AB．

查看试题解析
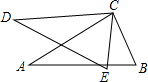24. 如果多边形的每个内角都比它相邻的外角的4倍多30°，求这个多边形的内角和及对角线的总条数．

查看试题解析
25. 如图①，四边形ABCD为正方形，点E，F分别在AB与BC上，且∠EDF=45°，易证：AE+CF=EF（不用证明）．

(1)、如图②，在四边形ABCD中，∠ADC=120°，DA=DC，∠DAB=∠BCD=90°，点E，F分别在AB与BC上，且∠EDF=60°．猜想AE，CF与EF之间的数量关系，并证明你的猜想；

(2)、如图③，在四边形ABCD中，∠ADC=2α，DA=DC，∠DAB与∠BCD互补，点E，F分别在AB与BC上，且∠EDF=α，请直接写出AE，CF与EF之间的数量关系，不用证明．

查看试题解析
26. 某街道改建工程指挥部，要对某路段工程进行招标，接到了甲、乙两个工程队的投标书．从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的 $\frac{2}{3}$ ；若由甲队先做10天，剩下的工程再由甲、乙两队合作30天可以完成.

(1)、求甲、乙两队单独完成这项工程各需多少天？

(2)、已知甲队每天的施工费用为0.84万元，乙队每天的施工费用为0.56万元，工程预算的施工费用为50万元．为缩短工期以减少对住户的影响，拟安排甲、乙两队合作完成这项工程，则工程预算的施工费用是否够用？若不够用，需追加预算多少万元？请给出你的判断并说明理由.

查看试题解析
27. 如图，在平面直角坐标系中，四边形ABCD是边长为5的正方形，顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA ， OB的长满足|OA﹣4|+（OB﹣3）²＝0．

(1)、求OA ， OB的长；

(2)、求点D的坐标；

(3)、在y轴上是否存在点P ，使△PAB是以AB为腰的等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析