黑龙江省鸡东县2018-2019学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（　　）

A、a²•a³=a⁶ B、（2a）²=2a² C、（a²）³=a⁶ D、（a+1）²=a²+1

查看试题解析
2. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若关于x的方程 $\frac{m - 1}{x - 1} - \frac{x}{x - 1} = 0$ 有增根，则m的值是（）

A、3 B、2 C、1 D、－1

查看试题解析
4. 在 $\frac{1}{x}$ ， $\frac{a^{2} b}{2}$ ，﹣3xy+y² ， $\frac{m - n}{4}$ ， $\frac{b - c}{5 + a}$ ，分式的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
5. 若把分式 $\frac{y}{x + y}$ 中的x和y都扩大2倍，则分式的值（　　）

A、扩大2倍 B、缩小4倍 C、缩小2倍 D、不变

查看试题解析
6. 下列二次根式中最简二次根式是（　　）

A、 $\sqrt{12 a}$ B、 $\sqrt{1 \frac{1}{3}}$ C、 $\sqrt{2}$ D、 $\sqrt{3 m^{2} n^{3}}$

查看试题解析
7. 若x²+kx+9是完全平方式，则k的值是（　　）

A、6 B、﹣6 C、9 D、6或﹣6

查看试题解析
8. 八年级学生去距学校10千米的博物馆参观，一部分学生骑自行车先走，过了20分钟后，其余学生乘汽车出发，结果他们同时到达，已知汽车的速度是骑车学生速度的2倍．设骑车学生的速度为x千米/小时，则所列方程正确的是（　　）

A、 $\frac{10}{x} - \frac{10}{2 x} = 20$ B、 $\frac{10}{2 x} - \frac{10}{x} = 20$ C、 $\frac{10}{x} - \frac{10}{2 x} = \frac{1}{3}$ D、 $\frac{10}{2 x} - \frac{10}{x} = \frac{1}{3}$

查看试题解析
9. 如图，等边三角形ABC中，D、E分别为AB、BC边上的两动点，且总使AD=BE，AE与CD交于点F，AG⊥CD于点G，则 $\frac{F G}{A F}$ =（　　）

A、 $\frac{1}{2}$ B、2 C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
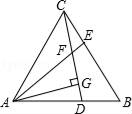10. 如图，∠AOB=120°，OP平分∠AOB，且OP=2．若点M，N分别在OA，OB上，且△PMN为等边三角形，则满足上述条件的△PMN有（）

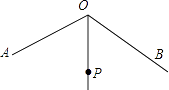A、1个 B、2个 C、3个 D、3个以上

查看试题解析

二、填空题

11. 科学家发现一种病毒的直径为 0.00000104米，用科学记数法表示为米.

查看试题解析
12. 当x时，分式 $\frac{x - 2}{3 x + 5}$ 有意义．

查看试题解析
13. 分解因式：4m²﹣16n²＝．

查看试题解析
14. 计算： $\sqrt{18} - \sqrt{32} =$ ．

查看试题解析
15. 如图，AD⊥BC，BD=CD，点C在AE的垂直平分线上，已知BD=2，AB=4，则DE= ．

查看试题解析
16. 已知 $x + \frac{1}{x} = 3$ ，则代数式 $x^{2} + \frac{1}{x^{2}}$ 的值为．

查看试题解析
17. 当x时，分式 $\frac{2 x + 1}{x^{2}}$ 的值为正．

查看试题解析
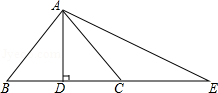18. 已知：如图，Rt△ABC中，∠BAC＝90°，AB＝AC ， D是BC的中点，AE＝BF ．若BC＝8，则四边形AFDE的面积是．

查看试题解析
19. 等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为．

查看试题解析
20. 如图，第1个图形有1个三角形，第2个图形中有5个三角形，第3个图形中有9个三角形，……，则第2019个图形中有个三角形．

查看试题解析

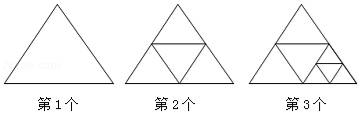
三、解答题

21. 计算：

(1)、4（x+y）（x﹣y）﹣（2x﹣y）²

(2)、（ $\sqrt{24}$ + $\sqrt{0.5}$ ）﹣（ $\sqrt{\frac{1}{8}}$ ﹣ $\sqrt{6}$ ）

查看试题解析
22. 解方程： $\frac{3}{x - 2} = \frac{2}{x} + \frac{6}{x^{2} - 2 x}$

查看试题解析
23. 先化简，再求值： $\frac{3 x - 6}{x^{2} + 4 x + 4} \div \frac{x - 2}{x + 2} - \frac{1}{x + 2}$ ，其中x= $\sqrt{2} - 2 \times {(- 1)}^{0}$ ．

查看试题解析
24. △ABC在平面直角坐标系中的位置如图．A、B、C三点在格点上．

(1)、作出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；

(2)、在y轴上找点D ，使得AD+BD最小，作出点D并写出点D的坐标．

查看试题解析
25. 已知 $\frac{1}{a} - \frac{1}{b} = 3$ ，求 $\frac{2 a + 3 a b - 2 b}{a - 2 a b - b}$ 的值．

查看试题解析
26. 已知a，b，c都是实数，且满足(2－a)²＋ $\sqrt{a^{2} + b + c} + | c + 8 |$ ＝0，且ax²＋bx＋c＝0，求代数式3x²＋6x＋1的值．

查看试题解析
27. 欧城物业为美化小区，要对面积为9600平方米的区域进行绿化，计划安排甲、乙两个园林队完成，已知甲园林队每天绿化面积是乙园林队每天绿化面积的2倍，并且甲、乙两园林队独立完成面积为800平方米区域的绿化时，甲园林队比乙园林队少用2天．

(1)、求甲、乙两园林队每天能完成绿化的面积分别是多少平方米．

(2)、物业每天需付给甲园林队的绿化费用为0.4万元，乙园林队的绿化费用为0.25万元，如果这次绿化总费用不超过10万元，那么欧城物业至少应安排甲园林队工作多少天？

查看试题解析
28. 已知△ABC为等边三角形，E为射线BA上一点，D为直线BC上一点，ED＝EC ．

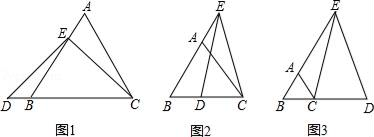(1)、当点E在AB的上，点D在CB的延长线上时（如图1），求证：AE+AC＝CD；

(2)、当点E在BA的延长线上，点D在BC上时（如图2），猜想AE、AC和CD的数量关系，并证明你的猜想；

(3)、当点E在BA的延长线上，点D在BC的延长线上时（如图3），请直接写出AE、AC和CD的数量关系．

查看试题解析