黑龙江哈尔滨市南岗区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2020-01-09 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点 关于 轴对称的点的坐标是( )A、 B、 C、 D、2. 使 有意义的x的取值范围是( )
A、x≤3 B、x<3 C、x≥3 D、x>33. 下列四个图案中,不是轴对称图案的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 若 是分式方程 的根,则 的值为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 若 是分式方程 的根,则 的值为( )
A、6 B、-6 C、4 D、-46. 下列运算正确的是( )A、 B、 C、 D、7. 若x,y的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A、 B、 C、 D、8. 若 , ,则 的值为( )A、 B、 C、 D、9. 甲、乙两地相距600km,乘高铁列车从甲地到乙地比乘特快列车少用4h,已知高铁列车的平均行驶速度是特快列车的3倍,设特快列车的平均行驶速度为xkm/h,根据题意可列方程为( )
A、 =4 B、 =4 C、 =4 D、 =4×210. 如图是由 个全等的长方形组成的大正方形,线段 的端点都在小长方形的顶点上,如果点 是某个小长方形的顶点,连接 , ,那么使 为等腰直角三角形的点 的个数是( ).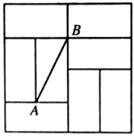 A、 个 B、 个 C、 个 D、 个
A、 个 B、 个 C、 个 D、 个二、填空题
-
11. 在人体血液中,红细胞直径约为 ,数据0.00077用科学记数法表示为 .12. 计算: =.13. 分解因式: .14. 分式 的值为0,那么x的值为 .
15. 化简: =.16. 不等式 的解集为.17. 我国南宋著名数学家秦九韶在他的著作《数学九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 , , ,则该三角形的面积为 .现已知 的三边长分别为 , , ,则 的面积为. 18. 已知 , ,则 的值为.19. 在 中, ,过点 作 交射线 于点 ,若 是等腰三角形,则 的大小为度.20. 如图,在 中, , ,点 在边 上, , ,点 , 分别是边 , 上的动点,连接 , ,则 的最小值为.
18. 已知 , ,则 的值为.19. 在 中, ,过点 作 交射线 于点 ,若 是等腰三角形,则 的大小为度.20. 如图,在 中, , ,点 在边 上, , ,点 , 分别是边 , 上的动点,连接 , ,则 的最小值为.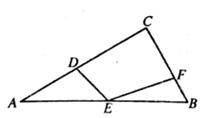
三、解答题
-
21.(1)、(2)、22. 先化简,再求代数式 的值,其中 .23. 如图,将边长为的形纸板沿虚线剪成面积分别为 , 的两个小正方形和两个长方形,已知边长为 的小正方形的面积为 ,拿掉边长为 的小正方形纸板后,将剩下的三块拼成新的长方形.
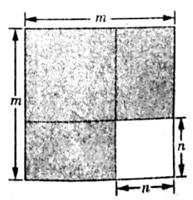 (1)、填空: = , =;(2)、求拼成的新长方形我的面积.24. 在 中, , ,点 是 的中点,点 是 上的一点(点 不与点 , 重合).过点 ,点 作直线 的垂线,垂足分别为点 和点 .
(1)、填空: = , =;(2)、求拼成的新长方形我的面积.24. 在 中, , ,点 是 的中点,点 是 上的一点(点 不与点 , 重合).过点 ,点 作直线 的垂线,垂足分别为点 和点 .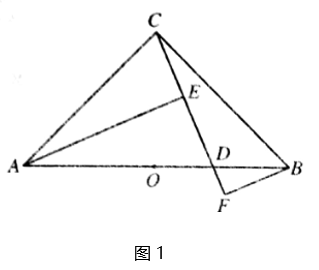
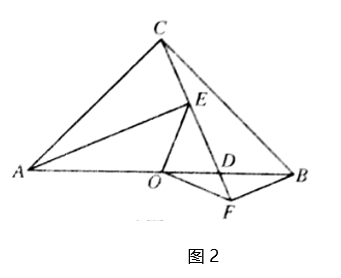 (1)、如图1,求证: ;(2)、如图2,连接 , ,请判断线段 与 之间的数量关系和位置关系,并说明理由.25. 市政府计划对城区道路进行改造,现安排甲、乙两个工程队共同完成.已知甲队的工作效率是乙队工作效率的 倍,甲队改造 米的道路比乙队改造同样长的道路少用 天.(1)、甲、乙两个工程队每天能改造道路的长度分别是多少米?(2)、若甲队工作一天的改造费用 万元,乙队工作一天的改造费用为 万元,如需改造的道路全长为 米,改造总费用不超过 万元,至少安排甲队工作多少天?26. 阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到 世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若 ,那么 叫做以 为底 的对数,记作: .比如指数式 可以转化为 ,对数式 可以转化为 .我们根据对数的定义可得到对数的一个性质: ( , , , );理由如下:设 M=m, ,则 , ,由对数的定义得 又 + .解决一下问题:(1)、将指数式 转化为对数式;(2)、证明 ( , , , );(3)、拓展运用:计算 =.27. 已知: 是 的高,且 .(1)、如图1,求证: ;
(1)、如图1,求证: ;(2)、如图2,连接 , ,请判断线段 与 之间的数量关系和位置关系,并说明理由.25. 市政府计划对城区道路进行改造,现安排甲、乙两个工程队共同完成.已知甲队的工作效率是乙队工作效率的 倍,甲队改造 米的道路比乙队改造同样长的道路少用 天.(1)、甲、乙两个工程队每天能改造道路的长度分别是多少米?(2)、若甲队工作一天的改造费用 万元,乙队工作一天的改造费用为 万元,如需改造的道路全长为 米,改造总费用不超过 万元,至少安排甲队工作多少天?26. 阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到 世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若 ,那么 叫做以 为底 的对数,记作: .比如指数式 可以转化为 ,对数式 可以转化为 .我们根据对数的定义可得到对数的一个性质: ( , , , );理由如下:设 M=m, ,则 , ,由对数的定义得 又 + .解决一下问题:(1)、将指数式 转化为对数式;(2)、证明 ( , , , );(3)、拓展运用:计算 =.27. 已知: 是 的高,且 .(1)、如图1,求证: ;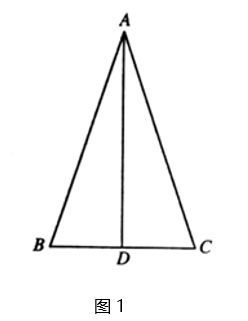 (2)、如图2,点E在AD上,连接 ,将 沿 折叠得到 , 与 相交于点 ,若BE=BC,求 的大小;
(2)、如图2,点E在AD上,连接 ,将 沿 折叠得到 , 与 相交于点 ,若BE=BC,求 的大小;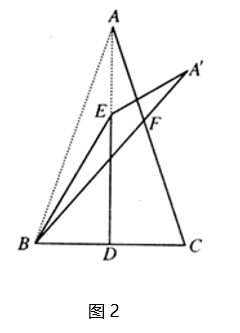 (3)、如图3,在(2)的条件下,连接 ,过点 作 ,交 的延长线于点 ,若 , ,求线段 的长.
(3)、如图3,在(2)的条件下,连接 ,过点 作 ,交 的延长线于点 ,若 , ,求线段 的长.