黑龙江省哈尔滨市松北区2019-2020学年九年级上学期数学期末考试试卷
试卷更新日期:2020-01-09 类型:期末考试
一、单选题
-
1. 2的相反数是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
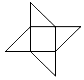 B、
B、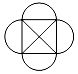 C、
C、 D、
D、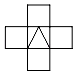 3. 下列运算正确的是A、 B、 C、 D、4. 如图所示物体的俯视图是( )
3. 下列运算正确的是A、 B、 C、 D、4. 如图所示物体的俯视图是( )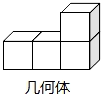 A、
A、 B、
B、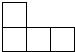 C、
C、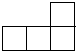 D、
D、 5. 反比例函数 的图象经过点(﹣2,3),则k的值为( )A、3 B、﹣ C、 D、﹣36. 一家公司招考员工,每位考生要在A、B、C、D、E这5道试题中随机抽出2道题回答,规定答对其中1题即为合格.已知某位考生会答A、B两题,则他合格的概率为( )A、 B、 C、 D、7. 关于x的方程kx2+2x﹣1=0有实数根,则k的取值范围是( )A、k≥﹣1 B、k≥﹣1且k≠0 C、k≤﹣1 D、k≤1且k≠08. 如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是( )A、10cm2 B、10πcm2 C、20cm2 D、20πcm29. 将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、y=(x-1)2+2 B、y=(x+1)2+2 C、y=(x-1)2-2 D、y=(x+1)2-210. 如图,以原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
5. 反比例函数 的图象经过点(﹣2,3),则k的值为( )A、3 B、﹣ C、 D、﹣36. 一家公司招考员工,每位考生要在A、B、C、D、E这5道试题中随机抽出2道题回答,规定答对其中1题即为合格.已知某位考生会答A、B两题,则他合格的概率为( )A、 B、 C、 D、7. 关于x的方程kx2+2x﹣1=0有实数根,则k的取值范围是( )A、k≥﹣1 B、k≥﹣1且k≠0 C、k≤﹣1 D、k≤1且k≠08. 如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是( )A、10cm2 B、10πcm2 C、20cm2 D、20πcm29. 将二次函数y=x2的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )A、y=(x-1)2+2 B、y=(x+1)2+2 C、y=(x-1)2-2 D、y=(x+1)2-210. 如图,以原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )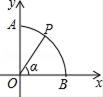 A、(sinα,sinα) B、(cosα,cosα) C、(cosα,sinα) D、(sinα,cosα)
A、(sinα,sinα) B、(cosα,cosα) C、(cosα,sinα) D、(sinα,cosα)二、填空题
-
11. 五年以来,我国城镇新增就业人数为66000000人,数据66000000用科学记数法表示为 .12. 分解因式: .13. 计算: -=
14. 已知一组数据2、7、9、10、x的平均数与众数相等,则x的值为 .15. 如图,O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=38º,则∠OAC的度数是.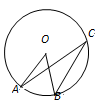 16. 不等式组 的解集是 .17. 已知一个多边形的内角和为540°,则这个多边形是边形.18. 在△ABC中,AB=2 ,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 .
16. 不等式组 的解集是 .17. 已知一个多边形的内角和为540°,则这个多边形是边形.18. 在△ABC中,AB=2 ,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 .
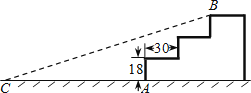
19.如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是cm.
 20. 如图,在 中, , , , , 的平分线相交于点E,过点E作 交AC于点F,则 ;
20. 如图,在 中, , , , , 的平分线相交于点E,过点E作 交AC于点F,则 ;
三、解答题
-
21. 先化简,再求代数式 ÷(1+ )的值,其中a=3tan30°+1.22. 如图,每个小正方形的边长都为1,△ABC的顶点都在格点上,回答下列问题:
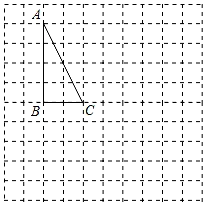 (1)、画出△ABC绕点B顺时针旋转90°的图形△A'BC′;(2)、求点C所形成的路径的长度.23. 某校为了解学生对“第二十届中国哈尔滨冰雪大世界”主题景观的了解情况,在全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图的不完整的两幅统计图:
(1)、画出△ABC绕点B顺时针旋转90°的图形△A'BC′;(2)、求点C所形成的路径的长度.23. 某校为了解学生对“第二十届中国哈尔滨冰雪大世界”主题景观的了解情况,在全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图的不完整的两幅统计图: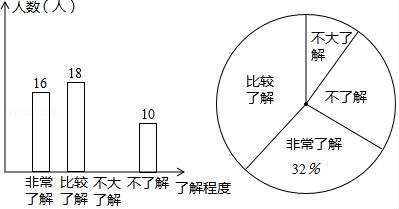 (1)、本次调查共抽取了多少名学生;(2)、通过计算补全条形图;(3)、若该学校共有750名学生,请你估计该学校选择“比较了解”项目的学生有多少名?24. 如图,直线y=x+3分别与x轴、y轴交于点A、C , 直线y=mx+ 分别与x轴、y轴交于点B、D , 直线AC与直线BD相交于点M(﹣1,b)
(1)、本次调查共抽取了多少名学生;(2)、通过计算补全条形图;(3)、若该学校共有750名学生,请你估计该学校选择“比较了解”项目的学生有多少名?24. 如图,直线y=x+3分别与x轴、y轴交于点A、C , 直线y=mx+ 分别与x轴、y轴交于点B、D , 直线AC与直线BD相交于点M(﹣1,b) (1)、不等式x+3≤mx+ 的解集为 .(2)、求直线AC、直线BD与x轴所围成的三角形的面积.25. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。(1)、求购买一个足球、一个篮球各需多少元?(2)、根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?26. 已知:BD为⊙O的直径,O为圆心,点A为圆上一点,过点B作⊙O的切线交DA的延长线于点F,点C为⊙O上一点,且AB=AC,连接BC交AD于点E,连接AC.
(1)、不等式x+3≤mx+ 的解集为 .(2)、求直线AC、直线BD与x轴所围成的三角形的面积.25. 某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元。(1)、求购买一个足球、一个篮球各需多少元?(2)、根据学校实际情况,需从体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?26. 已知:BD为⊙O的直径,O为圆心,点A为圆上一点,过点B作⊙O的切线交DA的延长线于点F,点C为⊙O上一点,且AB=AC,连接BC交AD于点E,连接AC.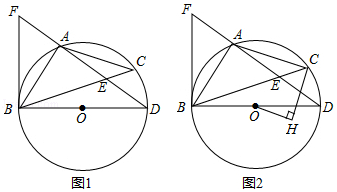 (1)、如图1,求证:∠ABF=∠ABC;(2)、如图2,点H为⊙O内部一点,连接OH,CH若∠OHC=∠HCA=90°时,求证:CH= DA;(3)、在(2)的条件下,若OH=6,⊙O的半径为10,求CE的长.27. 如图1,抛物线y=ax2﹣4ax+b经过点A(1,0),与x轴交于点B , 与y轴交于点C , 且OB=OC .
(1)、如图1,求证:∠ABF=∠ABC;(2)、如图2,点H为⊙O内部一点,连接OH,CH若∠OHC=∠HCA=90°时,求证:CH= DA;(3)、在(2)的条件下,若OH=6,⊙O的半径为10,求CE的长.27. 如图1,抛物线y=ax2﹣4ax+b经过点A(1,0),与x轴交于点B , 与y轴交于点C , 且OB=OC .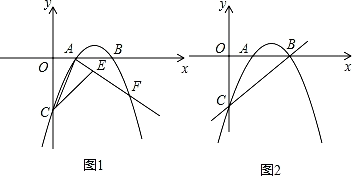 (1)、求抛物线的解析式;(2)、将△OAC沿AC翻折得到△ACE , 直线AE交抛物线于点P , 求点P的坐标;(3)、如图2,点M为直线BC上一点(不与B、C重合),连OM , 将OM绕O点旋转90°,得到线段ON , 是否存在这样的点N , 使点N恰好在抛物线上?若存在,求出点N的坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、将△OAC沿AC翻折得到△ACE , 直线AE交抛物线于点P , 求点P的坐标;(3)、如图2,点M为直线BC上一点(不与B、C重合),连OM , 将OM绕O点旋转90°,得到线段ON , 是否存在这样的点N , 使点N恰好在抛物线上?若存在,求出点N的坐标;若不存在,说明理由.