浙江省宁波市普通高中2020年保送生模拟测试数学试卷
试卷更新日期:2020-01-09 类型:中考模拟
一、选择题(每小题5分)
-
1. 设 是有理数, ,则正确的是( )A、 没有最小值 B、只有一个 使 取到最小值 C、有有限多个 (不止一个)使 取到最小值 D、有无穷多个 使 取到最小值2. 如图,点A在双曲线 上,且OA=4,过A作AC⊥ 轴,垂足为C,OA的垂直平分线交OC于B,则△ABC的周长为( )
 A、4 B、5 C、 D、3. 点D、E分别在AB、AC上,且AD=2BD,CE=2AE,若 =( ).
A、4 B、5 C、 D、3. 点D、E分别在AB、AC上,且AD=2BD,CE=2AE,若 =( ). A、12 B、13 C、14 D、154. 如图所示,二次函数 的图象与x轴负半轴相交与A、B两点, 是二次函数 图象上的一点,且 ,则 的值为( )
A、12 B、13 C、14 D、154. 如图所示,二次函数 的图象与x轴负半轴相交与A、B两点, 是二次函数 图象上的一点,且 ,则 的值为( ) A、 B、 C、 D、5. 如图,在△ABC中,AC=BC=2,D是BC的中点,过A,C,D三点的⊙O与AB边相切于点A,则⊙O的半径为( )
A、 B、 C、 D、5. 如图,在△ABC中,AC=BC=2,D是BC的中点,过A,C,D三点的⊙O与AB边相切于点A,则⊙O的半径为( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题(每小题5分)
-
6. 若关于 的分式方程 的解为非负数,则 的取值范围为.7. 设 ,(n为自然数),其中 与 分别表示 的整数部分和小数部分,如[2.5]=2, =0.5; , =0.4;则 =8. 已知:如图,矩形OABC中,点B的坐标为 ,双曲线 的一支与矩形两边AB,BC分别交于点E,F. 若将△BEF沿直线EF对折,B点落在y轴上的点D处,则点D的坐标是
 9. 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC. 若∠ABC的平分线BF交AD于点F, DE=4,DF=3,则AF的长为 .
9. 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E做直线l∥BC. 若∠ABC的平分线BF交AD于点F, DE=4,DF=3,则AF的长为 .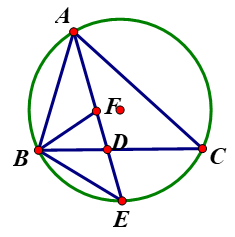
三、解答题(共30分,每题15分)
-
10. 已知,在平面直角坐标系xOy中,点A的坐标为(0,2),点P(m,n)是抛物线 上的一个动点.
 (1)、如图1,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA与PB的大小关系:PAPB(直接填写“>”“<”或“=”,不需解题过程);
(1)、如图1,过动点P作PB⊥x轴,垂足为B,连接PA,请通过测量或计算,比较PA与PB的大小关系:PAPB(直接填写“>”“<”或“=”,不需解题过程);
(2)、请利用(1)的结论解决下列问题:
①如图2,设C的坐标为(2,5),连接PC,AP+PC是否存在最小值?如果存在,求点P的坐标;如果不存在,简单说明理由;
②如图3,过动点P和原点O作直线交抛物线于另一点D,若AP=2AD,求直线OP的解析式.11. 对于平面直角坐标系xOy中的点P和⊙M,给出如下定义:若⊙M上存在两个点A,B,使AB=2PM,则称点P为⊙M的“美好点”. (1)、当⊙M半径为2,点M和点O重合时,
(1)、当⊙M半径为2,点M和点O重合时,1 点 中,⊙ 的“美好点”是;
2 点P为直线y=x+b上一动点,点P为⊙ 的“美好点”,求b的取值范围;
(2)、点M为直线y=x上一动点,以2为半径作⊙M,点P为直线y=4上一动点,点P为⊙M的“美好点”,求点M的横坐标m的取值范围.