河南省新乡市卫辉市2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 化简 $\sqrt{（ - 2 ）^{2}}$ 的结果是（）

A、－2 B、2 C、－4 D、4

查看试题解析
2. 下列计算正确的是 $($ $)$

A、 $4 a^{2} \div 2 a^{2} = 2 a^{2}$ B、 $- ($ $a^{3})^{2} = a^{6}$ C、 $(- 2 a) (- a) = 2 a^{2}$ D、 $(a - b) (- a - b) = a^{2} - b^{2}$

查看试题解析
3. 用反证法证明“在一个三角形中，至少有一个内角小于或等于60°”时应假设（）

A、三角形中有一个内角小于或等于60° B、三角形中有两个内角小于或等于60° C、三角形中有三个内角小于或等于60° D、三角形中没有一个内角小于或等于60°

查看试题解析
4. 要反映台州市某一周每天的最高气温的变化趋势，宜采用( )

A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布统计图

查看试题解析
5. 已知 $Δ A B C$ 的三边长分别为 $a 、 b 、 c$ ，且满足 ${(a － b)}^{2} ＋ | a^{2} ＋ b^{2} － c^{2} | ＝ 0$ ，则 $Δ A B C$ 的形状为（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形

查看试题解析
6. 某校学生参加体育兴趣小组情况的统计图如图所示，若参加人数最少的小组有25人，则参加人数最多的小组有（）

A、25人 B、35人 C、40人 D、100人

查看试题解析
7. 已知 $3^{a} = 1 ， 3^{b} = 2 ，$ 则 $3^{a + b}$ 的值为（）

A、1 B、2 C、3 D、27

查看试题解析
8. 如图，在 $∠ E C F$ 的两边上有点 $B 、 A 、 D$ ， $B C = B D = D A$ ，且 $∠ A D F = 75^{\circ}$ ，则 $∠ E C F$ 的度数为（）

A、 $15^{\circ}$ B、 $20^{\circ}$ C、 $25^{\circ}$ D、 $30^{\circ}$

查看试题解析
9. 如图，已知△ABC中，∠ABC=90°，AB=BC，过△ABC的顶点B作直线 $l$ ，且点A到 $l$ 的距离为2，点C到 $l$ 的距离为3，则AC的长是（）

A、 $\sqrt{13}$ B、 $\sqrt{20}$ C、 $\sqrt{26}$ D、5

查看试题解析
10. 已知AB=AC.如图，D、E为∠BAC的平分线上的两点，连接BD、CD、BE、CE；如图4， D、E、F为∠BAC的平分线上的三点，连接BD、CD、BE、CE、BF、CF；如图5， D、E、F、G为∠BAC的平分线上的四点，连接BD、CD、BE、CE、BF、CF、BG、CG……依此规律，第17个图形中有全等三角形的对数是（）

A、17 B、54 C、153 D、171

查看试题解析

二、填空题

11. 命题“对顶角相等”改写成如果…那么…形式为

查看试题解析
12. “阳光体育”活动在我市各校蓬勃开展，某校在一次大课间活动中抽查了10名学生每分钟跳绳次数，获得如下数据（单位：次）：83、89、93、99、117、121、130、146、158、188．其中跳绳次数大于100的频率是；

查看试题解析
13. 如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需添加一个条件是.

查看试题解析
14. 如图是放在地面上的一个长方体盒子，其中AB=18cm，BC=12cm，BF=10cm，点M在棱AB上，且AM=6cm，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程为.

查看试题解析
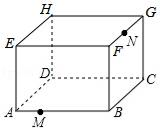15. 如图，△ABC中，∠A=90°，AB=3，AC=6，点D是AC边的中点，点P是BC边上一点，若△BDP为等腰三角形，则线段BP的长度等于.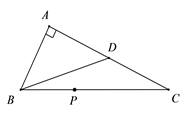

查看试题解析

三、解答题

16. 计算或因式分解：

(1)、计算： $(8 a^{3} - 4 a^{2}) \div 4 a$ ；

(2)、计算： $| - \frac{5}{2} | \times 2^{3} - \sqrt{4} \times \sqrt[3]{1000}$ ；

(3)、计算： $2 (a^{2} + 2) - (a + 1) (a - 1)$ ；

(4)、因式分解： $(a + 2) (a + 4) + 1$ ．

查看试题解析
17. 化简求值：[4(x²＋y)(x²－y)－(2x²－y)²]÷y，其中x= $\frac{1}{2}$ ，y=3.

查看试题解析
18. 如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F。

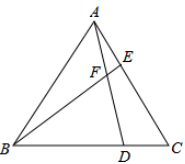
(1)、求证：△ABE≌△CAD；

(2)、求∠BFD的度数

查看试题解析
19. 如图，在△ABC中，∠C=90°，AC=6，BC=8.

(1)、用直尺和圆规作∠A的平分线，交BC于点D；（要求：不写作法，保留作图痕迹）

(2)、求S_△_ADC： S_△ADB的值.

查看试题解析
20. 某校为了解学生的安全意识情况，在全校范围内随机抽取部分学生进行问卷调查，根据调查结果，把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次，并绘制成如图9的两幅尚不完整的统计图.

根据以上信息，解答下列问题：

(1)、这次调查一共抽取了名学生；

(2)、请将条形统计图补充完整；

(3)、分别求出安全意识为“淡薄”的学生占被调查学生总数的百分比、安全意识为“很强”的学生所在扇形的圆心角的度数.

查看试题解析
21. 如图，矩形纸片ABCD中，AB=8，将纸片折叠，使顶点B落在边AD的E点上，BG=10，当折痕的另一端F在AB边上时，求△EFG的面积.

查看试题解析
22. 如图，两个等腰直角△ABC和△CDE中，∠ACB=∠DCE=90°．

(1)、观察猜想如图1，点E在BC上，线段AE与BD的数量关系，位置关系．

(2)、探究证明把△CDE绕直角顶点C旋转到图2的位置，（1）中的结论还成立吗？说明理由；

(3)、拓展延伸：把△CDE绕点C在平面内自由旋转，若AC=BC=13，DE=10，当A、E、D三点在直线上时，请直接写出AD的长．

查看试题解析
23. 已知，如图，在长方形ABCD中，AB=4，AD=6.延长BC到点E，使CE=3，连接DE.

(1)、DE的长为.

(2)、动点P从点B出发，以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P运动的时间为t秒，求当t为何值时，△ABP和△DCE全等？

(3)、若动点P从点B出发，以每秒1个单位的速度仅沿着BE向终点E运动，连接DP.设点P运动的时间为t秒，是否存在t，使△PDE为等腰三角形？若存在，请直接写出t的值；否则，说明理由.

查看试题解析