云南省玉溪市江川区2019年数学中考模拟试卷（三）
试卷更新日期：2020-01-09 类型：中考模拟
一、单选题
-
1. 实数2， ， ，0中，无理数是（ ）A、2 B、 C、 D、02. 某城市几条道路的位置关系如图所示，已知AB∥CD，AE与AB的夹角为48°，若CF与EF的长度相等，则∠C的度数为（ ）
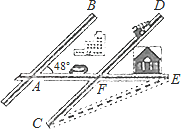A、48° B、40° C、30° D、24°3. 下列运算正确的是（ ）A、a﹣（b+c）＝a﹣b+c B、2a2•3a3＝6a5 C、a3+a3＝2a6 D、（x+1）2＝x2+14. 如图，是由7个大小相同的小正方体堆砌而成的几何体，若从标有①、②、③、④的四个小正方体中取走一个后，余下几何体与原几何体的主视图相同，则取走的正方体是（ ）
A、① B、② C、③ D、④5. 下列说法正确的是（ ）A、一个游戏的中奖概率是 则做10次这样的游戏一定会中奖 B、为了解全国中学生的心理健康情况，应该采用普查的方式 C、一组数据 8 ， 8 ， 7 ， 10 ， 6 ， 8 ， 9 的众数和中位数都是 8 D、若甲组数据的方差 S
=" 0.01" ，乙组数据的方差 s ＝ 0 .1 ，则乙组数据比甲组数据稳定
6. 实数a，b在数轴上对应点的位置如图所示，化简|a|+ 的结果是（ ）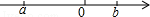
A、﹣2a-b B、2a﹣b C、﹣b D、b7. “赶陀螺”是一项深受人们喜爱的运动.如图所示是一个陀螺的立体结构图.已知底面圆的直径AB＝8 cm，圆柱的高BC＝6 cm，圆锥的高CD＝3 cm，则这个陀螺的表面积是（ ）
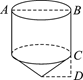A、68π cm2 B、74π cm2 C、84π cm2 D、100π cm28. 如图，已知A，B是反比例函数 图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C匀速运动，终点为C，过点P作PM⊥x轴，PN⊥y轴，垂足分别为M、N.设四边形OMPN的面积为S，点P运动的时间为t，则S关于t的函数图象大致为（ ）
A、
B、
C、
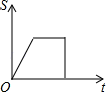D、
二、填空题
-
9. 化简： = ．10. 单项式9xmy3与单项式4x2yn是同类项，则m+n的值是.11. 这段时间，一个叫“学习强国”的理论学习平台火了，很多人主动下载、积分打卡，兴起了一股全民学习的热潮.据不完全统计，截止4月2号，华为官方应用市场“学习强国APP”下载量已达8830万次，请将8830万用科学记数法表示为是.12. 如图，已知Rt△ABC ， ∠C＝90°，BD是角平分线，BD＝5，BC＝4，则D点到AB的距离是 ．
13. 一块直角三角形板ABC，∠ACB＝90°，BC＝12 cm，AC＝8 cm，测得BC边的中心投影B1C1长为24 cm，则A1B1长为 cm.
14. 如图，正六边形ABCDEF的顶点B，C分别在正方形AMNP的边AM，MN上.若AB＝4，则CN＝.
三、解答题
-
15. 先化简，再求值： ，其中 .16. 如图，已知CA＝CD，AB＝DE，∠A＝∠D，求证：∠BCE＝∠ACD.
17. 昆明市某校学生会干部对校学生会倡导的“牵手滇西”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）.已知A、B两组捐款人数的比为1：5.组别
捐款额x/元
人数
A
1≤x＜10
a
B
10≤x＜20
100
C
20≤x＜30
D
30≤x＜40
E
40≤x＜50
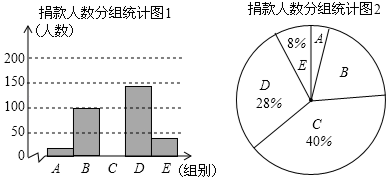
请结合以上信息解答下列问题.
(1)、a＝ ， 本次调查样本的容量是；(2)、先求出C组的人数，再补全“捐款人数分组统计图1”；(3)、根据统计情况，估计该校参加捐款的4500名学生有多少人捐款在20至40元之间.18. 探究：在一次聚会上，规定每两个人见面必须握手，且只握手1次
(1)、若参加聚会的人数为3，则共握手次：；若参加聚会的人数为5，则共握手次；(2)、若参加聚会的人数为n（n为正整数），则共握手次；(3)、若参加聚会的人共握手28次，请求出参加聚会的人数.(4)、拓展：嘉嘉给琪琪出题：
“若线段AB上共有m个点（含端点A，B），线段总数为30，求m的值.”
琪琪的思考：“在这个问题上，线段总数不可能为30”
琪琪的思考对吗？为什么？
19. 小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．(1)、如果小明第一题不使用“求助”，那么小明答对第一道题的概率是 ．(2)、如果小明将“求助”留在第二题使用，请用树状图或者列表来分析小明顺利通关的概率．(3)、从概率的角度分析，你建议小明在第几题使用“求助”．（直接写出答案）20. 为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．
(1)、求y与x的函数关系式；(2)、若在购买计划中，B种苗的数量不超过35棵，但不少于A种苗的数量，请设计购买方案，使总费用最低，并求出最低费用．
