广东省六校联盟2019-2020学年高三上学期文数第二次联考试卷

试卷更新日期：2020-01-09 类型：月考试卷

进入出卷网下载

一、单选题

1. 设全集 $U$ 是实数集 $R$ ， $M = {x | \log_{2} x > 1} ， N = {x | 1 < x < 3}$ ，则 $(∁_{U} M) \cap N =$ （）

A、 ${x | 2 < x < 3}$ B、 ${x | x < 3}$ C、 ${x | 1 < x \leq 2}$ D、 ${x | x \leq 2}$

查看试题解析
2. 复数 $z$ 满足 $2 + 3 i = z i$ （其中 $i$ 是虚数单位），则 $z$ 的虚部为（）

A、2 B、 $- 2$ C、3 D、 $- 3$

查看试题解析
3. 在 $Δ A B C$ 中， $A B = \sqrt{3}$ ， $A C = 1$ ， $∠ B = 30^{\circ}$ ，则 $∠ A =$ （）

A、 $60^{\circ}$ B、 $30^{\circ}$ 或 $90^{\circ}$ C、 $60^{\circ}$ 或 $120^{\circ}$ D、 $90^{\circ}$

查看试题解析
4. 设平面向量 $\vec{a} = (- 2, 1)$ ， $\vec{b} = (λ, 2)$ ，若 $\vec{a}$ 与 $\vec{b}$ 的夹角为锐角，则 $λ$ 的取值范围是（）

A、 $(- \frac{1}{2}, 2) \cup (2, + \infty)$ B、 $(- \infty, - 4) \cup (- 4, 1)$ C、 $(1, + \infty)$ D、 $(- \infty, 1)$

查看试题解析
5. 若 $a > 0$ ， $b > 0$ ，则“ $a + b \leq 8$ ”是“ $a b \leq 16$ ”的（）.

A、必要不充分条件 B、充分不必要条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 设 $a = \log_{3} 0.4$ ， $b = \log_{2} 3$ ，则（）

A、 $a b > 0$ 且 $a + b > 0$ B、 $a b < 0$ 且 $a + b > 0$ C、 $a b > 0$ 且 $a + b < 0$ D、 $a b < 0$ 且 $a + b < 0$

查看试题解析
7. 已知函数 $f (x) = {\begin{array}{l} 1 + x^{2} ， x \leq 0 \\ 1 ， x > 0 \end{array}$ ，若 $f (x - 4) > f (2 x - 3)$ ，则实数 $x$ 的取值范围是（）

A、 $(- 1 ， + \infty)$ B、 $(- \infty ， - 1)$ C、 $(- 1 ， 4)$ D、 $(- \infty ， 1)$

查看试题解析
8. 设等差数列 ${a_{n}}$ 前 $n$ 项和为 $S_{n}$ ，若 $a_{4} + S_{5} = 2$ ， $S_{7} = 14$ ，则 $a_{10} =$ （）

A、18 B、16 C、14 D、12

查看试题解析
9. 某几何体的三视图如图所示，则该几何体的体积为（）

A、 $\frac{7 π}{6}$ B、 $\frac{4 π}{3}$ C、 $2 π$ D、 $\frac{13 π}{6}$

查看试题解析
10. 函数 $f (x) = (\frac{2}{1 + e^{x}} - 1) \sin x$ 图象的大致形状是（）

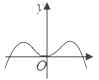A、 B、 C、 D、

查看试题解析
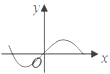11. 已知点A是抛物线 $x^{2} = 4 y$ 的对称轴与准线的交点，点B为抛物线的焦点，P在抛物线上且满足 $| P A | = m | P B |$ ，当 $m$ 取最大值时，点P恰好在以A、B为焦点的双曲线上，则双曲线的离心率为（）

A、 $\frac{\sqrt{2} + 1}{2}$ B、 $\sqrt{2} + 1$ C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\sqrt{5} - 1$

查看试题解析
12. 若存在唯一的正整数 $x_{0}$ ，使得不等式 $\frac{2 x}{e^{x}} - a x - a > 0$ 成立，则实数 $a$ 的取值范围是（）

A、 $(0 ， \frac{4}{3 e^{2}})$ B、 $(\frac{4}{3 e^{2}} ， \frac{1}{e})$ C、 $(0 ， \frac{1}{e})$ D、 $[\frac{4}{3 e^{2}} ， \frac{1}{e})$

查看试题解析

二、填空题

13. $\vec{a}$ 为单位向量， $\vec{b} \neq \vec{0}$ ，若 $\vec{a} ⊥ \vec{b}$ 且 $| \vec{a} - \vec{b} | = \frac{3}{2}$ ，则 $| \vec{b} | =$ .

查看试题解析
14. 若 $\tan (\frac{π}{4} - α) = - 2$ ，则 $\tan 2 α =$ .

查看试题解析
15. 若 $f (x) = \frac{1}{3} x^{3} - \frac{1}{2} f^{'} (1) x^{2} + x + \frac{1}{2}$ ，则曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程是．

查看试题解析
16. 已知三棱锥 $P - A B C$ 的四个顶点均在同一个球面上，底面 $Δ A B C$ 满足 $B A = B C = \sqrt{6}$ ， $∠ A B C = \frac{π}{2}$ ，若该三棱锥体积的最大值为3．则其外接球的体积为.

查看试题解析

三、解答题

17. 已知函数 $f (x) = {(\sqrt{3} \cos x + \sin x)}^{2} - 2 \sqrt{3} \sin 2 x$ ．

(1)、求函数 $f (x)$ 的最小值，并写出 $f (x)$ 取得最小值时自变量 $x$ 的取值集合；

(2)、若 $x \in [- \frac{π}{2} ， \frac{π}{2}]$ ，求函数 $f (x)$ 的单调减区间．

查看试题解析
18. 数列 ${a_{n}}$ 的前n项和记为 $S_{n}$ ， $a_{1} = 9$ ， $a_{n + 1} = 2 S_{n} + 9$ ， $n \in N^{*}$ ， $b_{1} = 1$ ， $b_{n + 1} - b_{n} = \log_{3} a_{n}$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、求证：对 $n \in N^{*}$ ，总有 $1 ⩽ \frac{1}{b_{1}} + \frac{1}{b_{2}} + \dots + \frac{1}{b_{n}} < 2$ ．

查看试题解析
19. 如图，在四棱锥 $P - A B C D$ 中，平面 $A B C D$ $⊥$ 平面 $P A D$ ， $A D ∥ B C$ ， $A B = B C = A P = \frac{1}{2} A D$ ， $∠ A D P = 30 °$ $∠ B A D = 90 °$ .

(1)、证明 $P D ⊥ P B$

(2)、设点 $M$ 在线段 $P C$ 上，且 $P M = \frac{1}{3} P C$ ，若 $Δ M B C$ 的面积为 $\frac{2 \sqrt{7}}{3}$ ，求四棱锥 $P - A B C D$ 的体积

查看试题解析
20. 在直角坐标系xOy中，动点P与定点 $F (1 ， 0)$ 的距离和它到定直线 $x = 4$ 的距离之比是 $\frac{1}{2}$ ，设动点P的轨迹为E．

(1)、求动点P的轨迹E的方程；

(2)、设过F的直线交轨迹E的弦为AB，过原点的直线交轨迹E的弦为CD，若 $C D ∥ A B$ ，求证： $\frac{| C D |^{2}}{| A B |}$ 为定值．

查看试题解析
21. 已知函数 $f (x) = \ln x + x + 1$ ， $g (x) = x^{2} + 2 x$ .
（Ⅰ）求函数 $y = f (x) - g (x)$ 的极值；

（Ⅱ）若实数 $m$ 为整数，且对任意的 $x > 0$ 时，都有 $f (x) - m g (x) \leq 0$ 恒成立，求实数 $m$ 的最小值.

查看试题解析
22. 在平面直角坐标系xOy中，曲线C的参数方程为 ${\begin{array}{l} x = 3 \cos α \\ y = \sin α \end{array}$ （a为参数），在以原点为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程为 $ρ \sin (θ - \frac{π}{4}) = \sqrt{2}$ .

(1)、求C的普通方程和l的倾斜角；

(2)、设点 $P (0,2)$ ，l和C交于A ， B两点，求 $| P A |+| P B |$ .

查看试题解析
23. 已知 $f (x) = 2 x^{2} + | 2 x - 1 | + a$

(1)、当 $a = - 3$ 时，求不等式 $f (x) > x^{2} + | x |$ 的解集；

(2)、若不等式 $f (x) \geq 0$ 的解集为实数集 $R$ ，求实数 $a$ 的取值范围.

查看试题解析