云南省玉溪市红塔区第一学区2019年数学中考三模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 2的相反数是（）

A、 $2$ B、 $- 2$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 我国首艘国产航母于2018年4月26日正式下水，排水量约为65000吨，将65000用科学记数法表示为（）

A、6.5×10^﹣4 B、6.5×10⁴ C、﹣6.5×10⁴ D、65×10⁴

查看试题解析
4. 若一个多边形的内角和为1440°，则这个多边形的边数是（）

A、8 B、10 C、12 D、14

查看试题解析
5. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（）

A、8cm B、5cm C、3cm D、2cm

查看试题解析
6. 下列运算正确的是（）

A、 ${(a - 3)}^{2} = a^{2} - 9$ B、 $a^{2} • a^{4} = a^{8}$ C、 $\sqrt{9} = \pm 3$ D、 $\sqrt[3]{- 8} = - 2$

查看试题解析
7. 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）

A、3：4 B、9：16 C、9：1 D、3：1

查看试题解析
8. 如图，在△ABC中，∠B＝90°，AB＝3cm，BC＝6cm，动点P从点A开始沿AB向点B以1cm/s的速度移动，动点Q从点B开始沿BC向点C以2cm/s的速度移动，若P，Q两点分别从A，B两点同时出发，P点到达B点运动停止，则△PBQ的面积S随出发时间t的函数关系图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 计算： $| - 2 | + {(π - 3)}^{0} =$ ．

查看试题解析
10. 若分式 $\frac{1}{x - 1}$ 有意义，则 $x$ 的取值范围是 .

查看试题解析
11. 如图，已知▱ABCD的对角线AC，BD交于点O，且AC=8，BD=10，AB=5，则△OCD的周长为.

查看试题解析
12. 一个三角形的两边长分别为3和6，第三边长是方程x²-10x+21=0的根，则三角形的周长为.

查看试题解析
13.
正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图的方式放置．点A₁ ， A₂ ， A₃ ， …和点C₁ ， C₂ ， C₃ ， …分别在直线y=x+1和x轴上，则点B₆的坐标是．

查看试题解析

三、解答题

14. 解不等式组 ${\begin{array}{l} 3 x + 1 \geq 5 x \\ \frac{x - 1}{2} > - 2 \end{array}$ .并写出所有整数解.

查看试题解析
15. 如图，正方形ABCD中，点E、F分别是边BC、CD上的点，且BE=CF
求证：

(1)、AE=BF

(2)、AE⊥BF

查看试题解析
16. 一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.

(1)、若降价3元，则平均每天销售数量为件；

(2)、当每件商品降价多少元时，该商店每天销售利润为1200元？

查看试题解析

17. 为了给游客提供更好的服务，某景区随机对部分游客进行了关于“景区服务工作满意度”的调查，并根据调查结果绘制成如下不完整的统计图表.

满意度	人数	所占百分比
非常满意	12	10%
满意	54	m
比较满意	n	40%
不满意	6	5%

根据图表信息，解答下列问题：

(1)、本次调查的总人数为，表中m的值为；

(2)、请补全条形统计图；

(3)、据统计，该景区平均每天接待游客约3600人，若将“非常满意”和“满意”作为游客对景区服务工作的肯定，请你估计该景区服务工作平均每天得到多少名游客的肯定.

查看试题解析

18. 如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向的B处，求此时轮船所在的B处与灯塔P的距离．（参考数据： $\sqrt{6}$ ≈2.449，结果保留整数）

查看试题解析
19. 端午节是我国传统佳节.小峰同学带了4个粽子（除粽馅不同外，其它均相同），其中有两个肉馅粽子、一个红枣馅粽子和一个豆沙馅粽子，准备从中任意拿出两个送给他的好朋友小悦.

(1)、用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果；

(2)、请你计算小悦拿到的两个粽子都是肉馅的概率.

查看试题解析
20. 已知：如图，AB是⊙O的直径，AB=4，点F，C是⊙O上两点，连接AC，AF，OC，弦AC平分∠FAB，∠BOC=60°，过点C作CD⊥AF交AF的延长线于点D，垂足为点D．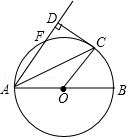

(1)、求扇形OBC的面积（结果保留π）；

(2)、求证：CD是⊙O的切线．

查看试题解析
21. 观察下面的变形规律： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ； $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ； $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ；….
解答下面的问题：

(1)、若n为正整数，请你猜想 $\frac{1}{n (n + 1)}$ ＝；

(2)、证明你猜想的结论；

(3)、求和： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{2009 \times 2010}$ .

查看试题解析
22. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c$ 交 $x$ 轴于点 $A (- 4 ， 0)$ 、 $B (2 ， 0)$ ，交 $y$ 轴于点 $C (0 ， 6)$ ，在 $y$ 轴上有一点 $E (0 ， - 2)$ ，连接 $A E$ .

(1)、求二次函数的表达式；

(2)、若点 $D$ 为抛物线在 $x$ 轴负半轴上方的一个动点，求 $Δ A D E$ 面积的最大值；

(3)、抛物线对称轴上是否存在点 $P$ ，使 $Δ A E P$ 为等腰三角形，若存在，请直接写出所有 $P$ 点的坐标，若不存在请说明理由.

查看试题解析