云南省曲靖市2019年数学中考二模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 火灾猛于虎!据应急管理部统计，2018年全国共接报火灾23.7万起，死亡1407人，伤798人，直接财产损失36.75亿元，其中36.75亿元用科学记数法表示正确的是（）

A、3.675×10⁹元 B、0.3675×10¹⁰元 C、3.675×10⁸元 D、36.75×10⁸元

查看试题解析
2. 下面几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、a¹²÷a⁶＝a⁶ B、（a^﹣²b）²＝a^﹣⁴b C、a³•a³＝2a⁶ D、（a²）³＝a⁵

查看试题解析
4. 小明在计算一个多边形的内角和时，漏掉了一个内角，结果算得800°，这个多边形应该是（）

A、六边形 B、七边形 C、八边形 D、九边形

查看试题解析
5. “倡导全民阅读”“推动国民素质和社会文明程度显著提高”已成为“十三五”时期的重要工作.某中学在全校学生中随机抽取了部分学生对2018年度阅读情况进行问卷调查，并将收集的数据统计如表

数量/本

15

11

8

4

3

2

人数

80

60

50

100

40

70

根据表中的信息判断，下列结论错误的是（）

A、该校参与调查的学生人数为400人 B、该校学生2018年度阅读书数量的中位数为4本 C、该校学生2018年度阅读书数量的众数为4本 D、该校学生2018年平均每人阅读8本书

查看试题解析
6. 观察下列图形，它们是按一定规律排列的，照此规律，第n个图形中“*“的个数是（）

A、4n+4 B、4n﹣4 C、4n D、n²

查看试题解析
7. 若等腰三角形的三边长均满足方程x²﹣7x+10＝0，则此三角形的周长为（）

A、9 B、12 C、9或12 D、不能确定

查看试题解析
8. 如图，在△ABC中，AB＝6，将△ABC绕点A通时针旋转40°后得到△ADE，点B经过的路径为 $\overset{⌢}{B D}$ ，则图中阴影部分的面积是（）

A、 $\frac{2}{3} π$ B、 $\frac{4}{3} π$ C、4π D、条件不足，无法计算

查看试题解析

二、填空题

9. ﹣5的相反数是．

查看试题解析
10. 在实数范围内，若 $\sqrt{9 - 2 x}$ 有意义，则x的取值范围是.

查看试题解析
11. 在实数范围内因式分解：2x³+8x²+8x＝

查看试题解析
12. 如图，将△ABC沿射线AB的方向平移到△DEF的位置，点A、B、C的对应点分别为点D、E、F，若∠ABC＝75°，则∠CFE＝

查看试题解析
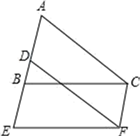13. 如图，反比例函数图象经过点A，过点A作AB⊥x轴，垂足为B，若△OAB的面积为3，则该反比例函数的解析式是.

查看试题解析
14. 若x²-4x+1=0，则 $x^{2} + \frac{1}{x^{2}}$ =.

查看试题解析

三、解答题

15. ${(- 1)}^{2019} + {(\frac{1}{2})}^{- 2} | 2 - \sqrt{12} | - {(\cos 45^{°} - π)}^{0}$

查看试题解析
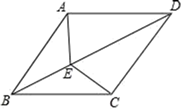
16. 如图，菱形ABCD中，E是对角线BD上的一点，连接EA、EC，求证：∠BAE＝∠BCE.

查看试题解析
17. 在某市举办的以“校园文明”为主题的中小学生手抄报比赛中，各学校认真组织初赛并按比例筛选出较好的作品参加全市决赛，所有参加市级决赛的作品均获奖，奖项分为一等奖.二等奖、三等奖和优秀奖.现从参加决赛的作品中随机抽取部分作品并将获奖结果绘制成如下两幅统计图请你根据图中所给信息解答下列问题：

(1)、一等奖所占的百分比是多少？三等奖的人数是多少？

(2)、求三等奖所对应的扇形圆心角的度数；

(3)、若参加决赛的作品有3000份，估计获得一等奖和二等奖的总人数有多少？

查看试题解析
18. “村村通公路政策，是近年来国家构建和谐社会，支持新农村建设的一项重大公共决策，是一项民心工程，惠民工程某镇政府准备向甲、乙两个工程队发包一段“村村通”工程建设项目，经调查：甲、乙两队单独完成该工程，乙队所需时间是甲队的2倍；甲、乙两队共同完成该工程需30天；若甲队每天所需劳务费用为2400元，乙队每天所需劳务费用为1500元，从节约资金的角度考虑，应选择哪个工程队更合算？

查看试题解析
19. 已知点A（1，1）在抛物线y＝x²+（2m+1）x﹣n﹣1上

(1)、求m、n的关系式；

(2)、若该抛物线的顶点在x轴上，求出它的解析式.

查看试题解析
20. “五一”小长假期间，小李一家想到以下四个5A级风景区旅游：A.石林风景区；B.香格里拉普达措国家公园；C.腾冲火山地质公园；D.玉龙雪山景区.但因为时间短，小李一家只能选择其中两个景区游玩

(1)、若小李从四个景区中随机抽出两个景区，请用树状图或列表法求出所有可能的结果；

(2)、在随机抽出的两个景区中，求抽到玉龙雪山风景区的概率.

查看试题解析

21. 精准扶贫”是巩固温饱成果，加快脱贫致富步伐，实现中华民族伟大复兴“中国梦”的重要保障某驻村帮扶小组因地制宜，积极筹集资金帮助所驻村建起了一个民族工艺品加工厂.现在，工厂计划加工100件A、B两种工艺品，现有生产这两种工艺品所需的甲种材料445米，乙种材料510米，毎生产1件A工艺品和1件B工艺品所需甲、乙两种材料及生产成本、利润如表

	甲材料（单位：米）	乙材料（单位：米）	生产成本（单位：元）	利润（单位：元）
A工艺品	0.4	0.6	60	25
B工艺品	0.5	0.3	45	20

设生产A种工艺品x件，1000件A、B两种工艺品销售完的总利润为y元，根据上述信息，解答下列问题

(1)、求y与x的函数解析式（也称关系式），并直接写出x的取值范围

(2)、若要使加工成本不超过53400元，则有几种加工方案？那种方案的利润最大？最大利润是多少？

查看试题解析

22. 如图，在△ABC中，AB＝AC，点D是BC边上一点，且AD＝BD，⊙O是△ACD的外接圆

(1)、求证：直线AB是⊙O的切线；

(2)、若AB＝10，BC＝16，求⊙O的半径.

查看试题解析
23. 如图，在矩形ABCD中，点E是BC边上的一个动点，沿着AE翻折矩形，使点B落在点F处若AB＝3，BC＝ $\sqrt{3}$ AB，解答下列问题：

(1)、在点E从点B运动到点C的过程中，求点F运动的路径长；

(2)、当点E是BC的中点时，试判断FC与AE的位置关系，并说明你的理由；

(3)、当点F在矩形ABCD内部且DF＝CD时，求BE的长.

查看试题解析

数量/本	15	11	8	4	3	2
人数	80	60	50	100	40	70