云南省普洱市宁洱县2019年数学中考模拟试卷（5月）

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 在函数 $y = \frac{1}{x - 2}$ 中，自变量x的取值范围是（）

A、x≠0 B、x＞2 C、x≥2 D、x≠2

查看试题解析
2. 如图所示的几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算中，正确的是（）

A、3a²﹣a²＝2 B、（a²）³＝a⁵ C、a²•a³＝a⁵ D、（2a²）²＝2a⁴

查看试题解析
4. 如图，已知a∥b，∠1＝50°，∠2＝90°，则∠3的度数为（）

A、40° B、50° C、150° D、140°

查看试题解析
5. 下列说法中错误的是（）

A、要了解某种灯管的使用寿命，一般采用抽样调查 B、一组数据的方差越小，这组数据的稳定性越差 C、数据1、2、3、4的中位数是2.5 D、数据3，4，5，6，6的众数是6

查看试题解析
6. 已知x，y满足关系式y＝ $\sqrt{x - 2} + \sqrt{2 - x}$ ﹣1，则y^x的值为（）

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
7. 已知圆锥的底面积为9πcm² ，母线长为6cm，则圆锥的侧面积是（）

A、18πcm² B、27πcm² C、18cm² D、27cm²

查看试题解析
8. 如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足S_△_PAB＝ $\frac{1}{3}$ S_矩形_ABCD ，则点P到A、B两点距离之和PA+PB的最小值为（）

A、 $\sqrt{29}$ B、 $\sqrt{34}$ C、5 $\sqrt{2}$ D、 $\sqrt{41}$

查看试题解析

二、填空题

9. ﹣2019的倒数是.

查看试题解析
10. 某种病毒变异后的直径约为0.000 000 56米，将这个数用科学记数法表示为米.

查看试题解析
11. 已知方程组 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = - 1 \end{array}$ ，则x﹣y的值为.

查看试题解析
12. 如图，在平面直角坐标系中，矩形ABCO的边CO、OA分别在x轴、y轴上，点E在边BC上，将该矩形沿AE折叠，点B恰好落在边OC上的F处.若OA＝8，CF＝4，则点E的坐标是.

查看试题解析
13. 如图，⊙O的半径为5cm，圆心O到AB的距离为3cm，则弦AB长为 cm．

查看试题解析
14. 已知点A在反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象上，过点A作AM⊥x轴于点M，△AMO的面积为3，则k＝.

查看试题解析

三、解答题

15. 计算： $\sqrt{9}$ ﹣（﹣1）²⁰¹⁹+（3.14﹣π）⁰﹣（ $\frac{1}{2}$ ）^﹣²

查看试题解析
16. 求出函数y＝ $\frac{x^{2} - 2 x}{x^{2} - 4} \div \frac{x + 2}{x^{2} + 4 x + 4}$ ﹣1与坐标轴围成的三角形的面积.

查看试题解析
17. 如图，在正方形ABCD中，AE，DF相交于点O且AF＝BE.

(1)、求证：△ABE≌△DAF；

(2)、求证：AE⊥DF.

查看试题解析
18. 为迎接2011年高中招生考试，某中学对全校九年级学生进行了一次数学摸底考试，并随机抽取了部分学生的测试成绩作为样本进行，绘制成了如下两幅不完整的统计图，请根据图中所给信息，下列问题：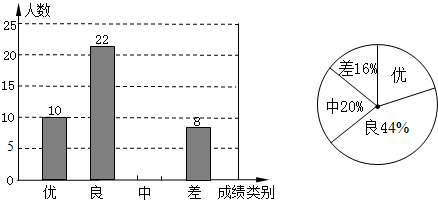

(1)、请将表示成绩类别为“中”的条形统计图补充完整；

(2)、在扇形统计图中，表示成绩类别为“优”的扇形所对应的圆心角是度；

(3)、学校九年级共有1000人参加了这次数学考试，估算该校九年级共有多少名学生的数学成绩可以达到优秀？

查看试题解析
19. 如图，电线杆AB直立于地面上，它的影子恰好照在土坡的坡面CD和地面BC上，若CD与地面成45°，∠A＝60°，CD＝4m， $B C = (4 \sqrt{6} - 2 \sqrt{2}) m$ ，则电线杆AB的长为多少米？

查看试题解析
20. 为了深入培养学生交通安全意识，加强实践活动，新华中学八年级（1）班和交警队联合举行了“我当一日小交警”活动，利用星期天到交通路口值勤，协助交通警察对行人、车辆及非机动车辆进行纠章.在这次实践活动中，若每一个路口安排5名学生，那么还剩下4人；若每个路口安排6人，那么最后一个路口不足3人，但不少于1人.

(1)、求新华中学八年级（1）班有多少名学生？

(2)、在值勤过程中，学生发现每辆汽车驶出路口后有三种方式前行：左转、直行、右转，而且每种前行方式的可能性相同.请通过画树形图或列表的方法，求连续驶出路口的两辆汽车前行路线相同的概率.

查看试题解析
21. 如图，△ABC是直角三角形，∠ACB＝90°，CD⊥AB于D，E是AC的中点，ED的延长线与CB的延长线交于点F.
求证：FD²＝FB•FC.

查看试题解析
22. 如图，抛物线y＝﹣x²+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线对称轴DE交x轴于点E，连接BD.

(1)、求经过A，B，C三点的抛物线的函数表达式；

(2)、点P是线段BD上一点，当PE＝PC时，求点P的坐标.

查看试题解析
23. 如图，A、B是⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合）、我们称∠APB是⊙O上关于点A、B的滑动角.

(1)、已知∠APB是⊙O上关于点A、B的滑动角，
①若AB是⊙O的直径，则∠APB＝°；

②若⊙O的半径是1，AB＝ $\sqrt{2}$ ，求∠APB的度数；

(2)、已知O₂是⊙O₁外一点，以O₂为圆心作一个圆与⊙O₁相交于A、B两点，∠APB是⊙O₁上关于点A、B的滑动角，直线PA、PB分别交⊙O₂于M、N（点M与点A、点N与点B均不重合），连接AN，试探索∠APB与∠MAN、∠ANB之间的数量关系.

查看试题解析