云南省怒江州兰坪县2019年数学中考二模试卷
试卷更新日期:2020-01-09 类型:中考模拟
一、单选题
-
1. 2011年国家启动实施农村义务教育学生营养改善计划,截至2014年4月,我省开展营养改善试点中小学达17580所,17580这个数用科学记数法可表示为( )A、 17.58×103 B、175.8×104 C、1.758×105 D、1.758×1042. 下列运算正确的是( )A、 B、 C、 D、3. 不等式组 的解在数轴上表示为 ( )A、
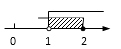 B、
B、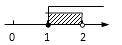 C、
C、 D、
D、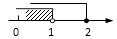 4. 下图是由大小相同的5个小正方体搭成的几何体,则它的主视图是( )
4. 下图是由大小相同的5个小正方体搭成的几何体,则它的主视图是( )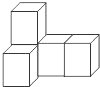 A、
A、 B、
B、 C、
C、 D、
D、 5. 方程x2﹣2x﹣4=0的根的情况( )A、只有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根6. 某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )
5. 方程x2﹣2x﹣4=0的根的情况( )A、只有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根6. 某校九年级数学模拟测试中,六名学生的数学成绩如下表所示,下列关于这组数据描述正确的是( )姓名
小红
小明
小东
小亮
小丽
小华
成绩(分)
110
106
109
111
108
110
A、众数是110 B、方差是16 C、平均数是109.5 D、中位数是1097. 如图,点A、B、C在⊙O上,CO的延长线交AB于点D,BD=BO,∠A=50°,则∠B的度数为( )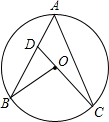 A、15° B、20° C、25° D、30°8. 如图,四边形OABC是矩形,等腰△ODE中,OE=DE,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y= 的图象上,OA=5,OC=1,则△ODE的面积为( )
A、15° B、20° C、25° D、30°8. 如图,四边形OABC是矩形,等腰△ODE中,OE=DE,点A、D在x轴的正半轴上,点C在y轴的正半轴上,点B、E在反比例函数y= 的图象上,OA=5,OC=1,则△ODE的面积为( )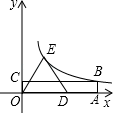 A、2.5 B、5 C、7.5 D、10
A、2.5 B、5 C、7.5 D、10二、填空题
-
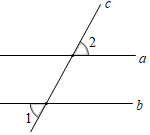
9. 的倒数是.10. 如图,a∥b,若∠1=40°,则∠2=度.
 11. 函数y= 中,自变量x的取值范围是.12. 已知一个圆锥底面直径为6,母线长为12,则其侧面展开图的圆心角为度.13. 观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,则第n个图中小黑点的个数为.
11. 函数y= 中,自变量x的取值范围是.12. 已知一个圆锥底面直径为6,母线长为12,则其侧面展开图的圆心角为度.13. 观察图1至图5中小黑点的摆放规律,并按照这样的规律继续摆放,则第n个图中小黑点的个数为.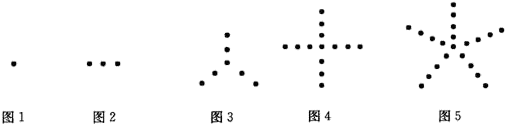
三、解答题
-
14. 已知x2+x-1=0,则3x2+3x-5=.15. 先化简,再求值: ÷(1﹣ ),其中a= ﹣2.16. 如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).
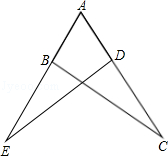 (1)、你添加的条件是(2)、添加条件后,请说明△ABC≌△ADE的理由.17. 为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题:
(1)、你添加的条件是(2)、添加条件后,请说明△ABC≌△ADE的理由.17. 为迎接2011年高中招生考试,某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行,绘制成了如下两幅不完整的统计图,请根据图中所给信息,下列问题: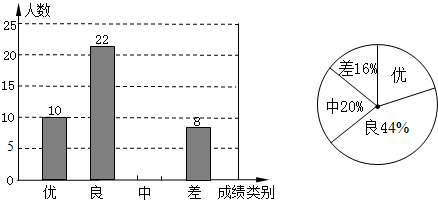 (1)、请将表示成绩类别为“中”的条形统计图补充完整;(2)、在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是度;(3)、学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?18. 有红、黄两个盒子,红盒子中装有编号分别为1、2、3、5的四个红球,黄盒子中装有编号为1、2、3的三个黄球.甲、乙两人玩摸球游戏,游戏规则为:甲从红盒子中每次摸出一个小球,乙从黄盒子中每次摸出一个小球,若两球编号之和为奇数,则甲胜,否则乙胜.(1)、试用列表或画树状图的方法,求甲获胜的概率;(2)、请问这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,试改动红盒子中的一个小球的编号,使游戏规则公平.19. 某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2015年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.(1)、实际每年绿化面积为多少万平方米?(2)、为加大创建力度,市政府决定从2018年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?20. 在如图所示的直角坐标系中,解答下列问题:
(1)、请将表示成绩类别为“中”的条形统计图补充完整;(2)、在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是度;(3)、学校九年级共有1000人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩可以达到优秀?18. 有红、黄两个盒子,红盒子中装有编号分别为1、2、3、5的四个红球,黄盒子中装有编号为1、2、3的三个黄球.甲、乙两人玩摸球游戏,游戏规则为:甲从红盒子中每次摸出一个小球,乙从黄盒子中每次摸出一个小球,若两球编号之和为奇数,则甲胜,否则乙胜.(1)、试用列表或画树状图的方法,求甲获胜的概率;(2)、请问这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,试改动红盒子中的一个小球的编号,使游戏规则公平.19. 某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2015年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.(1)、实际每年绿化面积为多少万平方米?(2)、为加大创建力度,市政府决定从2018年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?20. 在如图所示的直角坐标系中,解答下列问题: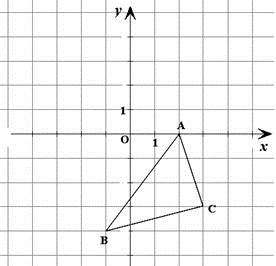 (1)、分别写出A、B两点的坐标;(2)、将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;(3)、求出线段B1A所在直线 l 的函数解析式,并写出在直线l上从B1到A的自变量x 的取值范围.21. 如图,某校数学兴趣小组的小明同学为测量位于玉溪大河畔的云铜矿业大厦AB的高度,小明在他家所在的公寓楼顶C处测得大厦顶部A处的仰角为45°,底部B处的俯角为30°.已知公寓高为40m,请你帮助小明计算公寓楼与矿业大厦间的水平距离BD的长度及矿业大厦AB的高度.(结果保留根号)
(1)、分别写出A、B两点的坐标;(2)、将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;(3)、求出线段B1A所在直线 l 的函数解析式,并写出在直线l上从B1到A的自变量x 的取值范围.21. 如图,某校数学兴趣小组的小明同学为测量位于玉溪大河畔的云铜矿业大厦AB的高度,小明在他家所在的公寓楼顶C处测得大厦顶部A处的仰角为45°,底部B处的俯角为30°.已知公寓高为40m,请你帮助小明计算公寓楼与矿业大厦间的水平距离BD的长度及矿业大厦AB的高度.(结果保留根号)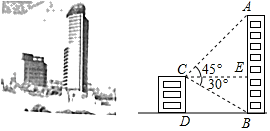 22. 已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,与x轴交于A、B两点,与y轴交于点C,其中A(﹣3,0)、C(0.﹣2).求这条抛物线的函数表达式.
22. 已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,与x轴交于A、B两点,与y轴交于点C,其中A(﹣3,0)、C(0.﹣2).求这条抛物线的函数表达式.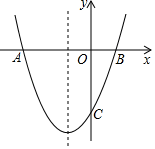 23. 如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2 , 矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn , OEFG围成,其中A1、G、B1在 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2 , C1D1⊥EF于H1 , FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn.
23. 如图1是一个用铁丝围成的篮框,我们来仿制一个类似的柱体形篮框.如图2,它是由一个半径为r、圆心角90°的扇形A2OB2 , 矩形A2C2EO、B2D2EO,及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn , OEFG围成,其中A1、G、B1在 上,A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上,C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上,EF⊥C2D2于H2 , C1D1⊥EF于H1 , FH1=H1H2=d,C1D1、C2D2、C3D3、CnDn依次等距离平行排放(最后一个矩形状框的边CnDn与点E间的距离应不超过d),A1C1∥A2C2∥A3C3∥…∥AnCn. (1)、求d的值;(2)、问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?
(1)、求d的值;(2)、问:CnDn与点E间的距离能否等于d?如果能,求出这样的n的值,如果不能,那么它们之间的距离是多少?