广东省六校联盟2019-2020学年高三上学期理数第二次联考试卷
试卷更新日期:2020-01-09 类型:月考试卷
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. “ ”是“ ”成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、不充分不必要条件3. 已知 ,则( )A、 B、 C、 D、4. 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )
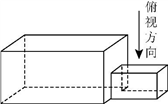 A、
A、 B、
B、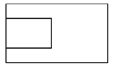 C、
C、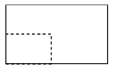 D、
D、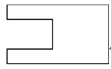 5. 函数 在 的图像大致为( )A、
5. 函数 在 的图像大致为( )A、 B、
B、 C、
C、 D、
D、 6. 已知非零向量 满足 且 ,则 与 的夹角为( )A、 B、 C、 D、7. 已知函数 的最小正周期为 , 且 ,则( )A、 在 单调递增 B、 在 单调递增 C、 在 单调递减 D、 在 单调递减8. 记等差数列 的前 项和为 ,若已知 ,则( )A、 B、 C、 D、9. 关于函数f(x)=tan|x|+|tanx|有下述四个结论:
6. 已知非零向量 满足 且 ,则 与 的夹角为( )A、 B、 C、 D、7. 已知函数 的最小正周期为 , 且 ,则( )A、 在 单调递增 B、 在 单调递增 C、 在 单调递减 D、 在 单调递减8. 记等差数列 的前 项和为 ,若已知 ,则( )A、 B、 C、 D、9. 关于函数f(x)=tan|x|+|tanx|有下述四个结论:① f(x)是偶函数; ② f(x)在区间 上单调递减;③ f(x)是周期函数; ④ f(x)图象关于 对称其中所有正确结论的编号是( )
A、①③ B、②③ C、①② D、③④10. 2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日 点的轨道运行. 点是平衡点,位于地月连线的延长线上.设地球质量为M1 , 月球质量为M2 , 地月距离为R, 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程: .设 ,由于 的值很小,因此在近似计算中 ,则r的近似值为( )A、 B、 C、 D、11. 已知三棱锥 的四个顶点在球 的球面上,点 分别是 的中点, ,则球 的表面积为( )A、 B、 C、 D、12. 已知函数 与 的图像上存在关于 轴对称的点,则实数 的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 已知正方形ABCD的边长为1,点E是AB边上的动点,则
 的值为 . 14. 已知 的内角 的对边分别为 , , ,若 ,则 .15. 数列 满足 , ,则 .16. 已知不等式 恒成立,则 的取值范围是.
的值为 . 14. 已知 的内角 的对边分别为 , , ,若 ,则 .15. 数列 满足 , ,则 .16. 已知不等式 恒成立,则 的取值范围是.三、解答题
-
17. 已知向量 , 设函数 .(1)、求 的最小正周期.(2)、求 在 上的最大值和最小值.18. 已知数列 的前 项和为 ,且 .(1)、求数列 的通项公式;(2)、记 ,数列 的前 项和为 ,求证: .19. 如图,菱形 的对角线 与 交于点O, ,点 分别在 上, , 交 于点 . 将 沿 折到△ 的位置, .
 (1)、证明: 平面 ;(2)、求二面角 的余弦值.20. 的内角 , , 所对边分别为 , , .已知 .(1)、求 ;(2)、若 为锐角三角形,且 ,求 面积的取值范围。21. 两县城 和 相距 ,现计划在两县城外位于线段 上选择一点 建造一个两县城的公共垃圾处理厂,已知垃圾处理厂对城市的影响度与所选地点到城市的的距离关系最大,其他因素影响较小暂时不考虑,垃圾处理厂对城 和城 的总影响度为对城 与城 的影响度之和. 记 点到城 的距离为 ,建在 处的垃圾处理厂对城 和城 的总影响度为 ,统计调查表明:垃圾处理厂对城 的影响度与所选地点到城 的距离的平方成反比,比例系数2.7;垃圾处理厂对城 的影响度与所选地点到城 的距离的平方成反比,比例系数为 ;且当垃圾处理厂 与城 距离为 时对城 和城 的总影响度为0.029.(1)、将 表示成 的函数;(2)、讨论⑴中函数的单调性,并判断在线段 上是否存在一点,使建在此处的垃圾处理厂对城 和城 的总影响度最小?若存在,求出该点到城 的距离;若不存在,说明理由.22. 已知函数 .(1)、若 ,求 的最小值;(2)、若 在 上单调递增,求 的取值范围;(3)、若 , 求证: .
(1)、证明: 平面 ;(2)、求二面角 的余弦值.20. 的内角 , , 所对边分别为 , , .已知 .(1)、求 ;(2)、若 为锐角三角形,且 ,求 面积的取值范围。21. 两县城 和 相距 ,现计划在两县城外位于线段 上选择一点 建造一个两县城的公共垃圾处理厂,已知垃圾处理厂对城市的影响度与所选地点到城市的的距离关系最大,其他因素影响较小暂时不考虑,垃圾处理厂对城 和城 的总影响度为对城 与城 的影响度之和. 记 点到城 的距离为 ,建在 处的垃圾处理厂对城 和城 的总影响度为 ,统计调查表明:垃圾处理厂对城 的影响度与所选地点到城 的距离的平方成反比,比例系数2.7;垃圾处理厂对城 的影响度与所选地点到城 的距离的平方成反比,比例系数为 ;且当垃圾处理厂 与城 距离为 时对城 和城 的总影响度为0.029.(1)、将 表示成 的函数;(2)、讨论⑴中函数的单调性,并判断在线段 上是否存在一点,使建在此处的垃圾处理厂对城 和城 的总影响度最小?若存在,求出该点到城 的距离;若不存在,说明理由.22. 已知函数 .(1)、若 ,求 的最小值;(2)、若 在 上单调递增,求 的取值范围;(3)、若 , 求证: .