云南省临沧市凤庆县2019届九年级5月学业水平模拟考试数学试卷
试卷更新日期:2020-01-09 类型:中考模拟
一、单选题
-
1. -2的倒数是( )A、2 B、-2 C、 D、2. 已知实数a、b满足a+b=2,ab= ,则a﹣b=( )A、1 B、﹣ C、±1 D、±3. 在函数 中,自变量x的取值范围是( )A、x≥l B、x>l C、x<l D、x≤14. 如图,A、B、C是小正方形的顶点,且每个小正方形的边长为l,则tan∠BAC为( )
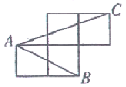 A、 B、 C、 D、15. 昆明市高新区某厂今年新招聘一批员工,他们中同文化程度的人数见下表:关于这组文化程度的人数数据,以下说法正确的是( )
A、 B、 C、 D、15. 昆明市高新区某厂今年新招聘一批员工,他们中同文化程度的人数见下表:关于这组文化程度的人数数据,以下说法正确的是( )文化程度
高中
大专
本科
硕士
博士
人数
9
17
20
9
5
A、众数是20 B、中位数是17 C、平均数是12 D、方差是266. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( ) A、 B、 C、 D、7. 观察图,下面所给几何体的俯视图是( )
A、 B、 C、 D、7. 观察图,下面所给几何体的俯视图是( )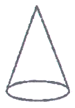 A、
A、 B、
B、 C、
C、 D、
D、 8. 正如我们小学学过的圆锥体积公式 ( 表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到 .祖冲之是世界上第一个把 计算到小数点后第7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把 计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内,即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习。下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于 ,则这个圆锥的高等于( ).A、 B、 C、 D、9. 2018年春节期间,云南接待游客约2882万人,旅游收入约193亿元,其中2882万用科学记数法表示为.10. 因式分解: =.11. 已知一元二次方程x2+mx+m﹣1=0有两个相等的实数根,则m= .12. 如图,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为.
8. 正如我们小学学过的圆锥体积公式 ( 表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到 .祖冲之是世界上第一个把 计算到小数点后第7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把 计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内,即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习。下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于 ,则这个圆锥的高等于( ).A、 B、 C、 D、9. 2018年春节期间,云南接待游客约2882万人,旅游收入约193亿元,其中2882万用科学记数法表示为.10. 因式分解: =.11. 已知一元二次方程x2+mx+m﹣1=0有两个相等的实数根,则m= .12. 如图,B(3,﹣3),C(5,0),以OC,CB为边作平行四边形OABC,则经过点A的反比例函数的解析式为.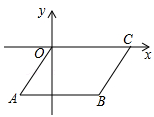 13. 等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .
13. 等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .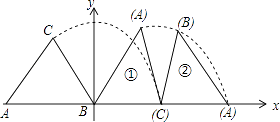 14. 如图所示,矩形纸片 中, ,按如图方式折叠,使点 与点 重合,折痕为 ,则 .
14. 如图所示,矩形纸片 中, ,按如图方式折叠,使点 与点 重合,折痕为 ,则 .
二、解答题
-
15. 计算:16. 先化简; ,再从-3,-2,0,2中选择一个合适的数作为x的值代入求值.17. 如图, , , .请写出 与 的数量关系,并证明你的结论.
 18. 随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示:
18. 随着社会的发展,通过微信朋友圈发布自己每天行走的步数已经成为一种时尚.“健身达人”小陈为了了解他的好友的运动情况.随机抽取了部分好友进行调查,把他们6月1日那天行走的情况分为四个类别:A(0~5000步)(说明:“0~5000”表示大于等于0,小于等于5000,下同),B(5001~10000步),C(10001~15000步),D(15000步以上),统计结果如图所示: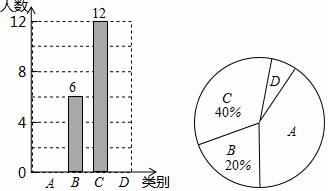
请依据统计结果回答下列问题:
(1)、本次调查中,一共调查了位好友.(2)、已知A类好友人数是D类好友人数的5倍.①请补全条形图;
②扇形图中,求“A”对应扇形的圆心角度数.
③若小陈微信朋友圈共有好友150人,请根据调查数据估计大约有多少位好友6月1日这天行走的步数超过10000步?
19. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,如图转盘甲和乙,方式一:转动转盘甲,指针指向A区域时,所购物品享受9折优惠,指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向的区域字母相同,所购物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区域的可能性相同(若指针指向分界线,则重新转动转盘). (1)、若顾客选择方式一,求享受9折优惠的概率.(2)、若顾客选择方式二,请用列表法或树状图法列出所有可能出现的结果:并求顾客享受8折优惠的概率.20. 五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.21. 如图,点A在⊙0上,点P是⊙0外一点.PA切⊙0于点A.连接OP交⊙0于点D,作AB⊥OP于点C,交⊙0于点B,连接PB.
(1)、若顾客选择方式一,求享受9折优惠的概率.(2)、若顾客选择方式二,请用列表法或树状图法列出所有可能出现的结果:并求顾客享受8折优惠的概率.20. 五一期间,某商场计划购进甲、乙两种商品,已知购进甲商品1件和乙商品3件共需240元;购进甲商品2件和乙商品1件共需130元.(1)、求甲、乙两种商品每件的进价分别是多少元?(2)、商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.21. 如图,点A在⊙0上,点P是⊙0外一点.PA切⊙0于点A.连接OP交⊙0于点D,作AB⊥OP于点C,交⊙0于点B,连接PB. (1)、求证:PB是⊙0的切线;(2)、若PC=9,AB=6 ,求图中阴影部分的面积.22. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)、求证:PB是⊙0的切线;(2)、若PC=9,AB=6 ,求图中阴影部分的面积.22. 如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.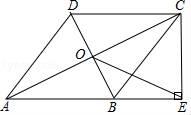 (1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.23. 如图,在平面直角坐标系中,抛物线经过点A(-3,0)、B(2,0)、C(0,4).
(1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.23. 如图,在平面直角坐标系中,抛物线经过点A(-3,0)、B(2,0)、C(0,4). (1)、求抛物线的解析式;(2)、在y轴上找一点D,使得△BOD与△AOC相似,请直接写出符合条件的点D的坐标;(3)、若AC与抛物线的对称轴交于点E,以A为圆心,AE长为半径作圆,⊙A与y轴的位置关系如何?请说明理由.(4)、过点E作⊙A的切线EG,交x轴于点G,请求出直线EG的解析式及G点坐标.
(1)、求抛物线的解析式;(2)、在y轴上找一点D,使得△BOD与△AOC相似,请直接写出符合条件的点D的坐标;(3)、若AC与抛物线的对称轴交于点E,以A为圆心,AE长为半径作圆,⊙A与y轴的位置关系如何?请说明理由.(4)、过点E作⊙A的切线EG,交x轴于点G,请求出直线EG的解析式及G点坐标.