云南省昆明市五华区2019届九年级数学中考二模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 其几何体的三视图如图所示，这个几何体是（）

A、三棱柱 B、四棱锥 C、四棱柱 D、圆锥

查看试题解析
2. 李老师给同学们布置了以下解方程的作业，作业要求是无实数根的方程不用解，不用解的方程是（）

A、x²﹣x＝0 B、x²+x＝0 C、x²+x﹣1＝0 D、x²+1＝0

查看试题解析
3. 不等式组 ${\begin{array}{l} 5 x - 3 > 2 \\ 4 - 2 x \leq 0 \end{array}$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
4. 仔细观察下列数字排列规律，则a＝（）

A、206 B、216 C、226 D、236

查看试题解析
5. 如图，是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图，下面关于该班50名同学一周锻炼时间的说法错误的是（）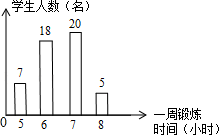

A、平均数是6 B、中位数是6.5 C、众数是7 D、平均每周锻炼超过6小时的人数占该班人数的一半

查看试题解析
6. 八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件：如图所示，在四边形ABCD中，点E，F分别在边BC，AD上，____，求证：四边形AECF是平行四边形. 你能在横线上填上最少且简捷的条件使结论成立吗？
条件分别是：①BE＝DF；②∠B＝∠D；③BAE＝∠DCF；④四边形ABCD是平行四边形.

其中A，B，C，D四位同学所填条件符合题目要求的是（）

A、①②③④ B、①②③ C、①④ D、④

查看试题解析
7. 某医疗器械公司接到400件医疗器械的订单，由于生产线系统升级，实际每月生产能力比原计划提高了30%，结果比原计划提前4个月完成交货.设每月原计划生产的医疗器械有x件，则下列方程正确的是（）

A、 $\frac{400}{x} - \frac{400}{(1 + 30 %) x}$ ＝4 B、 $\frac{400}{(1 + 30 %) x} - \frac{400}{x}$ ＝4 C、 $\frac{400}{x} - \frac{400}{(1 - 30 %) x}$ ＝4 D、 $\frac{400}{(1 - 30 %) x} - \frac{400}{x} = 4$

查看试题解析
8. 如图，正方形ABCD的边长为5，点A的坐标为（﹣4，0），点B在y轴上，若反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象过点C，则该反比例函数的表达式为（）

A、y＝ $\frac{3}{x}$ B、y＝ $\frac{4}{x}$ C、y＝ $\frac{5}{x}$ D、y＝ $\frac{6}{x}$

查看试题解析

二、填空题

9. ﹣2019的倒数是.

查看试题解析
10. 工匠绝技，精益求精，中国船舶重工的钳工顾秋亮凭着精到丝级的手艺，为海底探索者7000米级潜水器“蛟龙号”安装观察窗玻璃，成功地将玻璃与金属窗座之间的缝隙控制在0.2丝米以下已知1丝米＝0.0001，0.2丝米＝0.00002米，则用科学记数表示数据0.00002为.

查看试题解析
11. 函数y＝1﹣ $\sqrt{x}$ 的自变量x的取值范围是

查看试题解析
12. 如图所示，∠AOB＝70°，以点O为圆心，以适当长为半径作弧分别交OA，OB于C，D两点；分别以C，D为圆心，以大于 $\frac{1}{2}$ CD的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上取点M，连接MC、MD.若测得∠CMD＝40°，则∠MDB＝

查看试题解析
13. 将一个四边形的纸片一刀剪去一个角后，所得的多边形的内角之和是.

查看试题解析
14. 如图，等腰三角形ABC中，AB＝AC＝2，∠B＝75°，以C为旋转中心将△ABC顺时针旋转，当点B落在AB上点D处时，点A的对应点为E，则阴影部分面积为.

查看试题解析

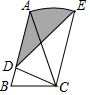
三、解答题

15. 先化简，再求值： $\frac{a^{2} - a}{a^{2} - 2 a + 1} \div (\frac{a}{a - 1} - 2)$ ，其中a＝2019⁰﹣（ $\frac{1}{2}$ ）^﹣¹

查看试题解析
16. 已知：AD是△ABC中BC边上的中线，延长AD至E，使DE＝AD，连接BE，求证：△ACD≌△EBD．

查看试题解析

17. 为了庆祝“五四”青年节，我市某中学举行了书法比赛，赛后随机抽查部分参赛同学成绩（满分为100分），并制作成图表如下

分数段	频数	频率
60≤x＜70	30	0.15
70≤x＜80	m	0.45
80≤x＜90	60	n
90≤x≤100	20	0.1

请根据以上图表提供的信息，解答下列问题：

(1)、这次随机抽查了学生；表中的数m＝， n＝；

(2)、请在图中补全频数分布直方图；

(3)、若绘制扇形统计图，分数段60≤x＜70所对应扇形的圆心角的度数是；

(4)、全校共有600名学生参加比赛，估计该校成绩不低于80分的学生有多少人？

查看试题解析

18. 如图，AB是长为10m，倾斜角为30°的自动扶梯，平台BD与大楼CE垂直，且与扶梯AB的长度相等，在B处测得大楼顶部C的仰角为65°，求大楼CE的高度（结果保留整数）.（参考数据：sin65°＝0.90，tan65°＝2.14）

查看试题解析
19. 合肥合家福超市为了吸引顾客，设计了一种促销活动：在三等分的转盘上依次标有“合”，“家”，“福”字样，购物每满200元可以转动转盘1次，转盘停下后，指针所指区域是“福”时，便可得到30元购物券（指针落在分界线上不计次数，可重新转动一次），一个顾客刚好消费400元，并参加促销活动，转了2次转盘.

(1)、求出该顾客可能获得购物券的最高金额和最低金额；

(2)、请用画树状图法或列表法求出该顾客获购物券金额不低于30元的概率.

查看试题解析

20. 已知抛物线y＝ax²+bx+c（a≠0）上部分点的横坐标x与纵坐标y的对应值如下表：

x	…	﹣3	﹣2	﹣1	0	1	2	3	…
y	…	$- \frac{5}{2}$	﹣4	$- \frac{9}{2}$	﹣4	$- \frac{5}{2}$	0	$\frac{7}{2}$	…

(1)、求该抛物线的表达式；

(2)、已知点E（4，y）是该抛物线上的点，点E关于抛物线的对称轴对称的点为点F，求点E和点F的坐标.

查看试题解析

21. 世界500强H公司决定购买某演唱会门票奖励部分优秀员工，演唱会的购票方式有以下两种，
方式一：若单位赞助广告费10万元，则该单位所购门票的价格为每张0.02万元（其中总费用＝广告赞助费+门票费）；

方式二：如图所示，设购买门票x张，总费用为y万元

(1)、求用购票“方式一”时y与x的函数关系式；

(2)、若H、A两家公司分别釆用方式一、方式二购买本场演唱会门票共400张，且A公司购买超过100张，两公司共花费27.2万元，求H、A两公司各购买门票多少张？

查看试题解析
22. 如图，△ABC中，以AC为直径的⊙O与边AB交于点D，点E为⊙O上一点，连接CE并延长交AB于点F，连接ED．

(1)、若∠B+∠FED=90°，求证：BC是⊙O的切线；

(2)、若FC=6，DE=3，FD=2，求⊙O的直径．

查看试题解析
23. 如图，点E，F分别在矩形ABCD的边AB，BC上，连接EF，将△BEF沿直线EF翻折得到△HEF，AB＝8，BC＝6，AE：EB＝3：1.

(1)、如图1，当∠BEF＝45°时，EH的延长线交DC于点M，求HM的长；

(2)、如图2，当FH的延长线经过点D时，求tan∠FEH的值；

(3)、如图3，连接AH，HC，当点F在线段BC上运动时，试探究四边形AHCD的面积是否存在最小值？若存在，求出四边形AHCD的面积的最小值；若不存在，请说明理由.

查看试题解析