云南省昆明市四校联考2019届九年级数学中考二模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 若a＞0，b＜0，那么a﹣b的值（）

A、大于零 B、小于零 C、等于零 D、不能确定

查看试题解析
2. 下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、3x²+4x²=7x⁴ B、（﹣x）^﹣⁹÷（﹣x）^﹣³=x^﹣⁶ C、x²﹣x²=1 D、﹣x（x²﹣x+1）=﹣x³﹣x²﹣x

查看试题解析
4. 为弘扬传统文化，某校初二年级举办传统文化进校园朗诵大赛，小明同学根据比赛中九位评委所给的某位参赛选手的分数，制作了一个表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（）
中位数
众数
平均数
方差
9.2
9.3
9.1
0.3

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
5. 某市从2017年开始大力发展“竹文化”旅游产业．据统计，该市2017年“竹文化”旅游收入约为2亿元．预计2019“竹文化”旅游收入达到2.88亿元，据此估计该市2018年、2019年“竹文化”旅游收入的年平均增长率约为（）

A、2% B、4.4% C、20% D、44%

查看试题解析
6. 关于x的方程（m﹣2）x²﹣4x+1＝0有实数根，则m的取值范围是（）

A、m≤6 B、m＜6 C、m≤6且m≠2 D、m＜6且m≠2

查看试题解析
7. 如图，二次函数y=ax²+bx+c（a≠0）的图象与x轴交于点A、B两点，与y轴交于点C，对称轴为直线x=﹣1，点B的坐标为（1，0），则下列结论：①AB=4；②b²﹣4ac＞0；③ab＜0；④a²﹣ab+ac＜0，其中正确的结论有（）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，将△ABC绕点C旋转60°得到△A′B′C′，已知AC=6，BC=4，则线段AB扫过的图形面积为（）

A、 $\frac{3 π}{2}$ B、 $\frac{8 π}{3}$ C、6π D、以上答案都不对

查看试题解析

二、填空题

9. 已知函数y= $\frac{\sqrt{2 x + 1}}{x - 2}$ ，则自变量x的取值范围是．

查看试题解析
10. 现今世界上较先进的计算机显卡每秒可绘制出27 000 000个三角形，且显示逼真，用科学记数法表示这种显卡每秒绘制出三角形个．

查看试题解析
11. $\sqrt{13}$ 的整数部分为a，则a²﹣3＝.

查看试题解析
12. 抛掷一枚质地均匀的骰子1次，朝上一面的点数不小于3的概率是．

查看试题解析
13. 已知：如图，△ABC的面积为12，点D、E分别是边AB、AC的中点，则四边形BCED的面积为.

查看试题解析
14. 现有八个大小相同的矩形，可拼成如图1、2所示的图形，在拼图2时，中间留下了一个边长为2的小正方形，则每个小矩形的面积是.

查看试题解析

三、解答题

15.

(1)、计算： ${(- 1)}^{- 2} + | 2 - \sqrt{3} | + 2 \cos 30^{0}$

(2)、解不等式组： ${\begin{array}{l} x - 2 \geq 1 \\ 2 (x - 1) < x + 3 \end{array}$

查看试题解析
16. 先化简，再求值： $\frac{2 x - 6}{x - 2} \div (\frac{5}{2 - x} - x - 2)$ ，其中x＝﹣1.

查看试题解析
17. 如图，在▱ABCD中，E是对角线BD上的一点，过点C作CF∥DB，且CF＝DE，连接AE，BF，EF．

(1)、求证：△ADE≌△BCF；

(2)、若∠ABE+∠BFC＝180°，则四边形ABFE是什么特殊四边形？说明理由．

查看试题解析

18. 某区为了解全区2800名九年级学生英语口语考试成绩的情况，从中随机抽取了部分学生的成绩（满分24分，得分均为整数），制成下表：

分数段（x分）	x≤16	17≤x≤18	19≤x≤20	21≤x≤22	23≤x≤24
人数	10	15	35	112	128

(1)、填空：

①本次抽样调查共抽取了名学生；

②学生成绩的中位数落在分数段；

③若用扇形统计图表示统计结果，则分数段为x≤16的人数所对应扇形的圆心角为°；

(2)、如果将21分以上（含21分）定为优秀，请估计该区九年级考生成绩为优秀的人数.

查看试题解析

19. 某工厂准备购买A、B两种零件，已知A种零件的单价比B种零件的单价多30元，而用900元购买A种零件的数量和用600元购买B种零件的数量相等.

(1)、求A、B两种零件的单价；

(2)、根据需要，工厂准备购买A、B两种零件共200件，工厂购买两种零件的总费用不超过14700元，求工厂最多购买A种零件多少件？

查看试题解析
20. 如图，一次函数 $y = k x + b$ 与反比例函数 $y = \frac{m}{x}$ 的图象交于A（1，4），B（4，n）两点.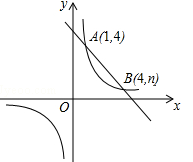

(1)、求反比例函数的解析式；

(2)、求一次函数的解析式；

(3)、点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小.

查看试题解析
21. 已知抛物线y＝ax²+bx+3与x轴交于点A（﹣1，0），B（3，0）.

(1)、求抛物线的解析式；

(2)、过点D（0， $\frac{7}{4}$ ）作x轴的平行线交抛物线于E，F两点，求EF的长；

(3)、当y≤ $\frac{7}{4}$ 时，直接写出x的取值范围是.

查看试题解析
22. 如图，以△ABC的一边AB为直径作⊙O，⊙O与BC边的交点D恰好为BC的中点，过点D作⊙O的切线交AC边于点F.

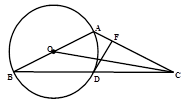(1)、求证：DF⊥AC；

(2)、若∠ABC=30°，求tan∠BCO的值.

查看试题解析
23. 如图

(1)、如图①，在矩形ABCD中，对角线AC与BD相交于点O，过点O作直线EF⊥BD，交AD于点E，交BC于点F，连接BE、DF，且BE平分∠ABD.
①求证：四边形BFDE是菱形；

②直接写出∠EBF的度数；

(2)、把(1)中菱形BFDE进行分离研究，如图②，点G、I分别在BF、BE边上，且BG=BI，连接GD，H为GD的中点，连接FH并延长，交ED于点J，连接IJ、IH、IF、IG.试探究线段IH与FH之间满足的关系，并说明理由；

(3)、把(1)中矩形ABCD进行特殊化探究，如图③，当矩形ABCD满足AB=AD时，点E是对角线AC上一点，连接DE、EF、DF，使△DEF是等腰直角三角形，DF交AC于点G.请直接写出线段AG、GE、EC三者之间满足的数量关系.

查看试题解析

中位数	众数	平均数	方差
9.2	9.3	9.1	0.3