云南省大理州祥云县2019年数学中考二模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

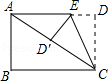
1. 风从海上来，潮起海之南，今年是海南建省办经济特区30周年.在过去的五年里，海南民生支出累计4613亿元。将数据4613亿用科学记数法表示为（）

A、4613×10⁸ B、461.3×10⁹ C、4.613×10¹¹ D、6.613×10¹⁰

查看试题解析
2. 若关于x的方程x²- $\sqrt{2}$ x+cosα=0有两个相等的实数根，则锐角α为（）.

A、30° B、45° C、60° D、75°

查看试题解析
3. 下列等式一定成立的是（）

A、a²+a³=a⁵ B、（a+b）²=a²+b² C、（2ab²）³=6a³b⁶ D、（x-a）（x-b）=x²-（a+b）x+ab

查看试题解析
4. 已知关于x的分式方程 $\frac{m}{x - 1}$ + $\frac{3}{1 - x}$ =1的解是非负数，则m的取值范围是（）

A、m＞2 B、m≥2 C、m≥2且m≠3 D、m＞2且m≠3

查看试题解析
5. 二次函数y=﹣x²+1的图像与x轴交于A、B两点，与y轴交于点C，下列说法错误的是（）

A、点C的坐标是（0，1） B、线段AB的长为2 C、△ABC是等腰直角三角形 D、当x＞0时，y随x增大而增大

查看试题解析
6. 如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处.若AB=3，AD=4，则ED的长为（）

A、 $\frac{3}{2}$ B、3 C、1 D、 $\frac{4}{3}$

查看试题解析
7. 如图，已知⊙O的半径为6cm，两弦AB与CD垂直相交于点E，若CE＝3cm，DE＝9cm，则AB＝（）

A、 $\sqrt{3}$ cm B、3 $\sqrt{3}$ cm C、5 $\sqrt{3}$ cm D、6 $\sqrt{3}$ cm

查看试题解析
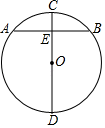8. 如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A₁B₁C，当A₁落在AB边上时，连接B₁B，取BB₁的中点D，连接A₁D，则A₁D的长度是（）

A、 $\sqrt{7}$ B、2 $\sqrt{2}$ C、3 D、2 $\sqrt{3}$

查看试题解析

二、填空题

9. 式子 $\frac{\sqrt{2 x + 1}}{x - 1}$ 有意义的x的取值范围是.

查看试题解析
10. 如图，△ABC是以AB为斜边的直角三角形，AC=4，BC=3，P为AB上一动点，且PE⊥AC于E，PF⊥BC于F，则线段EF长度的最小值是。

查看试题解析
11. 将抛物线y＝－2(x＋1)²－3先向左平移2个单位，再向上平移5个单位后，所得抛物线的表达式为 .

查看试题解析
12. 已知抛物线 $y = - 2 {(x + 1)}^{2} - 3$ 与直线 $y_{2} = k x + m$ 相交于A（-2，3）、B（3，-1）两点，则 $y_{1} \geq y_{2}$ 时x的取值范围是.

查看试题解析
13. 在平面直角坐标系中，对于平面内任一点（m，n），规定以下两种变换：
（ 1 ）f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；

（ 2 ）g（m，n）=（﹣m，﹣n），如g （2，1）=（﹣2，﹣1）

按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（﹣3，2）]=.

查看试题解析
14. 如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（3，4）为圆心，1为半径的圆上运动，且始终满足∠BPC＝90°，则a的最大值是.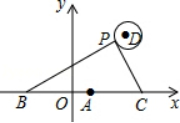

查看试题解析

三、解答题

15. 计算： ${(\frac{1}{3})}^{- 2} + {(π - 2014)}^{0} + sin 60^{0} + | \sqrt{3} - 2 |$ .

查看试题解析
16. 先化简，再求值： $\frac{x - 1}{x^{2} - 9} \div (\frac{x}{x - 3} - \frac{5 x - 1}{x^{2} - 9})$ ，其中x=3tan30°+1．

查看试题解析
17. 某调查小组采用简单随机抽样方法，对某市部分中小学生一天中阳光体育运动时间进行了抽样调查，并把所得数据整理后绘制成如下的统计图：

(1)、该调查小组抽取的样本容量是多少？

(2)、求样本学生中阳光体育运动时间为1.5小时的人数，并补全占频数分布直方图；

(3)、请估计该市中小学生一天中阳光体育运动的平均时间．

查看试题解析
18. 一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．

(1)、从中任意摸出1个球，恰好摸到红球的概率是；

(2)、先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．

查看试题解析
19. 如图，已知四边形ABCD是矩形，延长AB至点F，连结CF，使得CF=AF，过点A作AE⊥FC于点E.

(1)、求证：AD=AE.

(2)、连结CA，若∠DCA=70°，求∠CAE的度数.

查看试题解析
20. 如图，直线y=kx+b与双曲线 $y = \frac{m}{x}$ （x﹤0）相交于A（-4，a）、B（-1，4）两点.

(1)、求直线和双曲线的解析式；

(2)、在y轴上存在一点P，使得PA+PB的值最小，求点P的坐标.

查看试题解析
21. 我区注重城市绿化提高市民生活质量，新建林荫公园计划购买甲、乙两种树苗共800株，甲种树苗每株12元，乙种树苗每株15元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．

(1)、若购买这两种树苗共用去10500元，则甲、乙两种树苗各购买多少株？

(2)、若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？

(3)、在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．

查看试题解析
22. 如图，在△ABC中，AB=AC，以AC为直径的⊙O交BC于点D，交AB于点E，过点D作DF⊥AB，垂足为F，连接DE．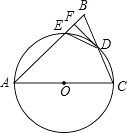

(1)、求证：直线DF与⊙O相切；

(2)、若AE=7，BC=6，求AC的长．

查看试题解析
23. 如图，在平面直角坐标系中，直线 $y = - \frac{4}{3} x + 8$ 与 $x$ 轴， $y$ 轴分别交于点A、B，抛物线 $y = a x^{2} - 4 a x + c$ 经过点A和点B，与x轴的另一个交点为C，动点D从点A出发，以每秒1个单位长度的速度向O点运动，同时动点E从点B出发，以每秒2个单位长度的速度向A点运动，设运动的时间为t秒，0﹤t﹤5.

(1)、求抛物线的解析式；

(2)、当t为何值时，以A、D、E为顶点的三角形与△AOB相似；

(3)、当△ADE为等腰三角形时，求t的值；

(4)、抛物线上是否存在一点F，使得以A、B、D、F为顶点的四边形是平行四边形？若存在，直接写出F点的坐标；若不存在，说明理由.

查看试题解析