云南省楚雄州双柏县2019年数学中考二模试卷
试卷更新日期:2020-01-09 类型:中考模拟
一、单选题
-
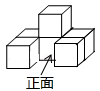
1. 下列运算正确的是( )A、4a2÷2a2=2 B、﹣a2•a3=a6 C、 D、2. 某商品打九折后价格为a元,则原价为( )元.A、a B、10%a C、 D、3. 某市在“扫黑除恶”专项斗争宣传活动中,共16000人参与,将16000用科学记数法表示为( )人.A、1.6×105 B、1.6×104 C、0.16×105 D、16×1034. 六个大小相同的正方体搭成的几何体如图所示,其俯视图是( )
 A、
A、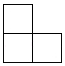 B、
B、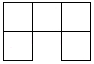 C、
C、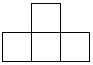 D、
D、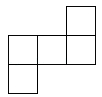 5. 不等式组 的解集是( )A、x<﹣2 B、﹣2<x≤1 C、x≤﹣2 D、x≥﹣26. 如图,在 中, , ,则 的度数是( )
5. 不等式组 的解集是( )A、x<﹣2 B、﹣2<x≤1 C、x≤﹣2 D、x≥﹣26. 如图,在 中, , ,则 的度数是( ) A、 B、 C、 D、7. 在一次数学测试中,某学校小组6名同学的成绩(单位:分)分别为65,82,86,82,76,95,关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是82 C、方差8.4 D、平均数是818. 如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( )
A、 B、 C、 D、7. 在一次数学测试中,某学校小组6名同学的成绩(单位:分)分别为65,82,86,82,76,95,关于这组数据,下列说法错误的是( )A、众数是82 B、中位数是82 C、方差8.4 D、平均数是818. 如图,在△ABC中,点D是边AB上的一点,∠ADC=∠ACB,AD=2,BD=6,则边AC的长为( ) A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
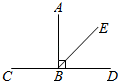
9. ﹣2019的倒数是.10. 分解因式4ab﹣2a2﹣2b2=.11. 函数 的自变量x的取值范围是.12. 如图,AB⊥CD于点B,BE是∠ABD的平分线,则∠CBE的度数为度.
 13. 已知,正比例函数y=kx与反比例函数 的图象有一个交点P(2,m),则正比例函数y=kx的解析式为.14. 观察下列一组数: , , , , ,…,它们是按一定规律排列的,那么这一组数的第n个数是 .
13. 已知,正比例函数y=kx与反比例函数 的图象有一个交点P(2,m),则正比例函数y=kx的解析式为.14. 观察下列一组数: , , , , ,…,它们是按一定规律排列的,那么这一组数的第n个数是 .
三、解答题
-
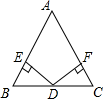
15. 计算:16. 已知,如图,D是△ABC的BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:AB=AC.
 17. 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
17. 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止). (1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、分别求出李燕和刘凯获胜的概率.18. 阅读有助于提高孩子的学习兴趣和积极性,但近年来出现很多中学生在学校看武侠小说的现象,某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生在校看武侠小说”这一现象的看法,统计整理并制作了如下的条形与扇形统计图.依据图中信息,解答下列问题:
(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、分别求出李燕和刘凯获胜的概率.18. 阅读有助于提高孩子的学习兴趣和积极性,但近年来出现很多中学生在学校看武侠小说的现象,某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生在校看武侠小说”这一现象的看法,统计整理并制作了如下的条形与扇形统计图.依据图中信息,解答下列问题: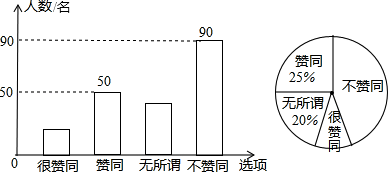 (1)、本次调查的学生家长有名,“不赞同”初中生在校看武侠小说的家长所对应的圆心角度数是;(2)、请补全条形统计图(标上柱高数值);(3)、该学校共3000名学生家长,请估计该校抱“不赞同”态度的学生家长人数.19. 商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示:
(1)、本次调查的学生家长有名,“不赞同”初中生在校看武侠小说的家长所对应的圆心角度数是;(2)、请补全条形统计图(标上柱高数值);(3)、该学校共3000名学生家长,请估计该校抱“不赞同”态度的学生家长人数.19. 商场进了一批家用空气净化器,成本为1200元/台.经调查发现,这种空气净化器每周的销售量y(台)与售价x(元/台)之间的关系如图所示: (1)、请写出这种空气净化器每周的销售量y与 售价x的函数关系式(不写自变量的范围);(2)、若空气净化器每周的销售利润为W(元),则当售价为多少时,可获得最大利润,此时的最大利润是多少?20. 如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)、请写出这种空气净化器每周的销售量y与 售价x的函数关系式(不写自变量的范围);(2)、若空气净化器每周的销售利润为W(元),则当售价为多少时,可获得最大利润,此时的最大利润是多少?20. 如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.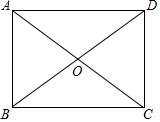 (1)、求证:平行四边形ABCD是矩形;(2)、请添加一个条件使矩形ABCD为正方形.21. 某小区为“创建文明城市,构建和谐社会”.更好的提高业主垃圾分类的意识,业主委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱.若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.(1)、问:购买1个温馨提示牌和1个垃圾箱各需多少元?(2)、如果需要购买温馨提示牌和垃圾箱共10个,费用不超过800元,问:最多购买垃圾箱多少个?22. 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM,垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)、求证:平行四边形ABCD是矩形;(2)、请添加一个条件使矩形ABCD为正方形.21. 某小区为“创建文明城市,构建和谐社会”.更好的提高业主垃圾分类的意识,业主委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱.若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.(1)、问:购买1个温馨提示牌和1个垃圾箱各需多少元?(2)、如果需要购买温馨提示牌和垃圾箱共10个,费用不超过800元,问:最多购买垃圾箱多少个?22. 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM,垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.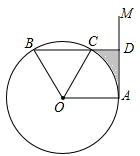 (1)、求证:AM是⊙O的切线;(2)、若⊙O的半径为4,求图中阴影部分的面积(结果保留π和根号).23. 如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.
(1)、求证:AM是⊙O的切线;(2)、若⊙O的半径为4,求图中阴影部分的面积(结果保留π和根号).23. 如图,在直角坐标系xOy中,二次函数y=x2+(2k﹣1)x+k+1的图象与x轴相交于O、A两点.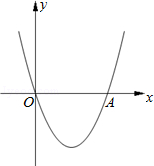 (1)、求这个二次函数的解析式;(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;(3)、对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.
(1)、求这个二次函数的解析式;(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;(3)、对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由.