新疆乌鲁木齐市九十八中2019届九年级下学期数学中考二模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果股票指数上涨 30 点记作+30，那么股票指数下跌 20 点记作（）

A、﹣20 B、+20 C、﹣10 D、+10

查看试题解析
2. 如图，直线a∥b，直角三角形如图放置，∠DCB=90°，若∠1+∠B=65°，则∠2的度数为（）

A、 $20^{\circ}$ B、 $25^{\circ}$ C、 $30^{\circ}$ D、 $35^{\circ}$

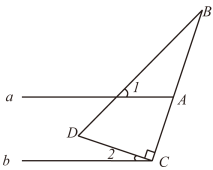查看试题解析
3. 下列计算正确的是（）

A、5a⁴•2a＝7a⁵ B、（﹣2a²b）²＝4a²b² C、2x（x﹣3）＝2x²﹣6x D、（a﹣2）（a+3）＝a²﹣6

查看试题解析
4. 由6个大小相同的小正方体搭成的几何体，被小颖拿掉2个后，得到如图①所示的几何体，图②是原几何体的三视图.请你判断小颖拿掉的两个小正方体原来放在（）

A、1号的前后 B、2号的前后 C、3号的前后 D、4号的左右

查看试题解析

5. 甲，乙两班举行电脑汉字输入速度比赛，参加学生每分钟输入汉字的个数经统计计算后填人下表：

班级	人数	中位数	方差	平均字数
甲	55	149	191	135
乙	55	151	110	135

某同学根据上表分析得出如下结论：①甲，乙两班学生成绩的平均水平相同；②乙班优秀的人数多于甲班优秀的人数（每分钟输入汉字数≥150个为优秀）；③甲班的成绩的波动情况比乙班的成绩的波动大.上述结论正确的是（）

A、①②③ B、①② C、①③ D、②③

查看试题解析

6. 关于x的一元二次方程ax²+3x﹣2=0有两个不相等的实数根，则a的值可以是（）

A、0 B、﹣1 C、﹣2 D、﹣3

查看试题解析
7. 为积极响应“传统文化进校园”的号召，某市某中学举行书法比赛，为奖励获奖学生，学校购买了一些钢笔和毛笔，钢笔单价是毛笔单价的1.5倍，购买钢笔用了1200元，购买毛笔用1500元，购买的钢笔支数比毛笔少20支，钢笔，毛笔的单价分别是多少元？如果设毛笔的单价为x元/支，那么下面所列方程正确的是（）

A、 $\frac{1200}{1.5 x} - \frac{1500}{x} = 20$ B、 $\frac{1500}{x} - \frac{1200}{1.5 x} = 20$ C、 $\frac{1500}{x} = 20 - \frac{1200}{1.5 x}$ D、 $\frac{1200}{x} - \frac{1500}{1.5 x} = 20$

查看试题解析
8. 如图，AB是⊙O的弦，CD是⊙O的直径，CD＝15，CD⊥AB于M，如果sin∠ACB＝ $\frac{3}{5}$ ，则AB＝（）

A、24 B、12 C、9 D、6

查看试题解析
9. 如图，矩形ABCD中，AB=10，BC=5，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（）

A、5 $\sqrt{5}$ B、10 $\sqrt{5}$ C、10 $\sqrt{3}$ D、15 $\sqrt{3}$

查看试题解析

二、填空题

10. 分解因式：4m²﹣16n²＝．

查看试题解析
11. 在一个袋子中装有大小相同的4个小球，其中1个蓝色，3个红色，从袋中随机摸出个，则摸到的是蓝色小球的概率为

查看试题解析
12. 如图，正比例函数y=kx与反比例函数y= $\frac{6}{x}$ 的图象有一个交点A(2，m)，AB⊥x轴于点B，平移直线y=kx使其经过点B，得到直线l，则直线l对应的函数表达式是 .

查看试题解析
13. 有一人患了流感，经过两轮传染后共有64人患了流感，那么每轮传染中平均一个人传染给个人.

查看试题解析
14. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝．如图所示的弦图中，中间的小正方形ABCD的边长为1，分别以A，C为圆心，1为半径作圆弧，则图中阴影部分的面积为．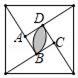

查看试题解析
15. 如图，以半圆中的一条弦BC（非直径）为对称轴将弧BC折叠后与直径AB交于点D，若 $\frac{A D}{B D}$ ＝ $\frac{2}{3}$ ，且AB＝10，则CB的长为.

查看试题解析

三、解答题

16. 计算：| $\sqrt{3}$ -2|+2^﹣¹﹣cos60°﹣(1﹣ $\sqrt{2}$ )⁰.

查看试题解析
17. 计算：

(1)、﹣（a²b）³+2a²b•（﹣3a²b）²

(2)、（a+2b﹣c）（a﹣2b+c）

(3)、已知6x﹣5y=10，求[（﹣2x+y）（﹣2x﹣y）﹣（2x﹣3y）²]÷4y的值．

查看试题解析
18. 已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点.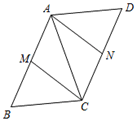

(1)、求证：四边形AMCN是平行四边形；

(2)、若AC＝BC＝5，AB＝6，求四边形AMCN的面积.

查看试题解析
19. “食品安全”受到全社会的广泛关注，济南市某中学对部分学生就食品安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题：

(1)、接受问卷调查的学生共有人，扇形统计图中“基本了解”部分所对应扇形的圆心角为；

(2)、请补全条形统计图；

(3)、若该中学共有学生900人，请根据上述调查结果，估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数；

(4)、若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.

查看试题解析
20. 为庆祝改革开放40周年，深圳举办了灯光秀，某数学兴趣小组为测量“平安金融中心”AB的高度，他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后，测得“平安中心”AB的顶部A处的仰角为60°，（如图）.已知C、D、B三点在同一水平直线上，且CD=400米，DB=200米.

（参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62， $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

(1)、求大厦DE的高度；

(2)、求平安金融中心AB的高度.

查看试题解析
21. 小明和小亮分别从甲地和乙地同时出发，沿同一条路相向而行，小明开始跑步，中途改为步行，到达乙地恰好用40min.小亮骑自行车以300m/min的速度直接到甲地，两人离甲地的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示，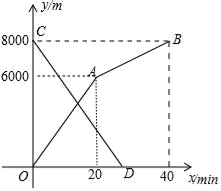

(1)、甲、乙两地之间的路程为m，小明步行的速度为m/min；

(2)、求小亮离甲地的路程y关于x的函数表达式，并写出自变量x的取值范围；

(3)、求两人相遇的时间.

查看试题解析
22. 如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP＝CB.

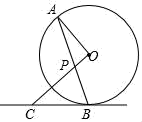(1)、求证：BC是⊙O的切线；

(2)、若OA＝5，OP＝3，求CB的长；

(3)、设△AOP的面积是S₁ ， △BCP的面积是S₂ ，且 $\frac{S_{1}}{S_{2}} = \frac{10}{9}$ .若⊙O的半径为4，BP＝ $\frac{6 \sqrt{5}}{5}$ ，求tan∠CBP.

查看试题解析
23. y＝﹣2x+4直线交x轴于点A，交y轴于点B，抛物线y＝﹣ $\frac{m}{2}$ （x﹣m）（x﹣6）（m＞0）经过点A，交x轴于另一点C，如图所示.

(1)、求抛物线的解析式.

(2)、设抛物线的顶点为D，连接BD，AD，CD，动点P在BD上以每秒2个单位长度的速度由点B向点D运动，同时动点Q在线段CA上以每秒3个单位长度的速度由点C向点A运动，当其中一个点到达终点停止运动时，另一个点也随之停止运动，设运动时间为t秒.PQ交线段AD于点E.
①当∠DPE＝∠CAD时，求t的值；

②过点E作EM⊥BD，垂足为点M，过点P作PN⊥BD交线段AB或AD于点N，当PN＝EM时，求t的值.

查看试题解析