新疆乌鲁木齐市多校联考2019年数学中考模拟试卷（5月）

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 在0，1，﹣ $\frac{1}{2}$ ，﹣1四个数中，最小的数是（）

A、0 B、1 C、 $\frac{1}{2}$ D、﹣1

查看试题解析
2. 如图，CD//AB，AC⊥BC，∠ACD=60°，那么∠B的度数是（）

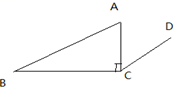A、60° B、40° C、45° D、30°

查看试题解析
3. 下列计算正确的是（）

A、2a﹣a＝1 B、﹣2a³÷（﹣a）＝a² C、a²•a³＝a⁶ D、（a³）²＝a⁶

查看试题解析
4.
如图，是某个几何体从不同方向看到的形状图（视图），这个几何体的表面能展开成下面的哪个平面图形？（　　）

A、 B、 C、 D、

查看试题解析
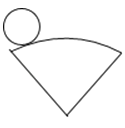5. 用配方法解方程x²+2x﹣1＝0时，配方结果正确的是（）

A、（x+2）²＝2 B、（x+1）²＝2 C、（x+2）²＝3 D、（x+1）²＝3

查看试题解析
6. 如图，在圆O中，点A、B、C在圆上，∠OAB＝50°，则∠C的度数为（）

A、30° B、40° C、50° D、60°

查看试题解析
7. 期中考试后，班里有两位同学议论他们小组的数学成绩，小晖说：“我们组考分是82分的人最多”，小聪说：“我们组的7位同学成绩排在最中间的恰好也是82分”.上面两位同学的话能反映出的统计量是（）

A、众数和平均数 B、平均数和中位数 C、众数和方差 D、众数和中位数

查看试题解析
8. 某市为解决部分市民冬季集中取暖问题，需铺设一条长4000米的管道，为尽量减少施工对交通造成的影响，施工时“…”，设实际每天铺设管道x米，则可得方程 $\frac{4000}{x - 10} - \frac{4000}{x}$ ＝20，根据此情景，题中用“…”表示的缺失的条件应补为（）

A、每天比原计划多铺设10米，结果延期20天完成 B、每天比原计划少铺设10米，结果延期20天完成 C、每天比原计划多铺设10米，结果提前20天完成 D、每天比原计划少铺设10米，结果提前20天完成

查看试题解析
9. 如图，边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′，边B′C′与DC交于点O，则四边形AB′OD的周长是（）

A、2 $\sqrt{2}$ B、3 C、 $\sqrt{2}$ D、1+ $\sqrt{2}$

查看试题解析

二、填空题

10. 分解因式：3ax²+6axy+3ay²＝.

查看试题解析
11. 式子 $\sqrt{2 - x}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
12. 一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球个．

查看试题解析
13. 将一个面积是120m²的矩形的长减少2m，就变成了正方形，则原来的长是m.

查看试题解析
14. 如图，直线AB经过原点O，与双曲线y= $\frac{k}{x}$ （k≠0）交于A、B两点，AC⊥y轴于点C，且△ABC的面积是8，则k的值是.

查看试题解析
15. 古希腊数学家把1、3、6、10、15、21、…叫做三角形数，其中1是第一个三角形数，3是第二个三角形数，6是第三个三角形数，…，依此类推，第10个三角形数是.

查看试题解析

三、解答题

16. 计算： $2^{- 1} - 2 cos 45 ° + {(π - 3)}^{0} + | - \frac{1}{2} |$ .

查看试题解析
17. 先化简，再求值： $(x + 1) (x - 1) + x (2 - x) + {(x - 1)}^{2}$ ，其中 $x = 2 \sqrt{3}$ .

查看试题解析
18. 在Rt△ABC中，∠BAC= 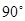，D是BC的中点，E是AD的中点．过点A作AF∥BC交BE的延长线于点F．

(1)、求证：△AEF≌△DEB；

(2)、证明四边形ADCF是菱形；

(3)、若AC=4，AB=5，求菱形ADCFD 的面积．

查看试题解析
19.
如图，在一笔直的海岸线l上有A、B两个码头，A在B的正东方向，一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处，此时从B码头测得小船在它的北偏东45°的方向．求此时小船到B码头的距离（即BP的长）和A、B两个码头间的距离（结果都保留根号）．

查看试题解析

20. 某校为了调查初三男生和女生周日学习用时情况，随机抽取了初三男生和女生各50人，对他们的周日学习时间进行了统计，分别得到了初三男生的学习时间的频率分布表和女生学习时间的频率分布直方图（学习时间x，单位：小时，0≤x≤6）.

男生周日学习时间频率表

学习时间	频率
0≤x＜1	0.34
1≤x＜2	0.36
2≤x＜3	0.38
3≤x＜4	0.22
4≤x＜5	0.14
5≤x＜6	0.06

(1)、请你判断该校初三年级周日学习用时较长的是男生还是女生，并说明理由；

(2)、从这100名学生中周日学习用时在5≤x≤6内的学生中抽取2人，求恰巧抽到一男一女的概率.

查看试题解析

21. A、B两地相距150km，甲、乙两人先后从A地出发向B地行驶，甲骑摩托车匀速行驶，乙开汽车且途中速度只改变一次，如图表示的是甲、乙两人之间的距离S关于时间t的函数图象（点F的实际意义是乙开汽车到达B地），请根据图象解答下列问题：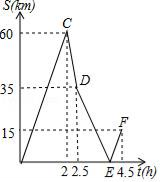

(1)、求出甲的速度；

(2)、求出乙前后两次的速度，并求出点E的坐标；

(3)、当甲、乙两人相距10km时，求t的值．

查看试题解析
22. 如图，在△ABC中，BE是它的角平分线，∠C＝90°，D在AB边上，以DB为直径的半圆O经过点E，交BC于点F.

(1)、求证：AC是⊙O的切线；

(2)、已知sinA＝ $\frac{1}{2}$ ，⊙O的半径为4，求图中阴影部分的面积.

查看试题解析
23. 如图1，抛物线 $y = x^{2} + b x + c$ 交x轴于点 $A (- 3 ， 0)$ ， $B (2 ， 0)$ ，交y轴于点C.

(1)、求抛物线的解析式；

(2)、如图2，D点坐标为 $(2 \sqrt{3} ， 0)$ ，连结 $D C .$ 若点H是线段DC上的一个动点，求 $O H + \frac{1}{2} H C$ 的最小值.

(3)、如图3，连结AC，过点B作x轴的垂线l，在第三象限中的抛物线上取点P，过点P作直线AC的垂线交直线l于点E，过点E作x轴的平行线交AC于点F，已知 $P E = C F$ .
$①$ 求点P的坐标；

$②$ 在抛物线 $y = x^{2} + b x + c$ 上是否存在一点Q，使得 $∠ Q P C = ∠ B P E$ 成立？若存在，求出Q点坐标；若不存在，请说明理由.

查看试题解析