江苏省盐城市东台市2019年数学中考模拟试卷(5月)
试卷更新日期:2020-01-09 类型:中考模拟
一、单选题
-
1. 8的立方根等于( )A、 2 B、-2 C、±2 D、2. 下列运算中,结果正确的是( )A、a4+a4=a8 B、a3•a2=a5 C、a8÷a2=a4 D、(-2a2)3=-6a63. 使 有意义的x的取值范围是( )A、x> B、x>- C、x≥ D、x≥-4. 如图,由5个完全相同的小正方体组合成的几何体,它的俯视图为( )
 A、
A、 B、
B、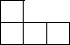 C、
C、 D、
D、 5. 如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是( )
5. 如图,BC是⊙O的直径,A是⊙O上的一点,∠OAC=32°,则∠B的度数是( )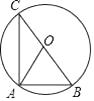 A、58° B、60° C、64° D、68°6. 如图,正方形ABCD的顶点A、D分别在x轴、y轴的正半轴上,若反比例函数y= (x>0)的图象经过另外两个顶点B、C,且点B(6,n),(0<n<6),则k的值为( )
A、58° B、60° C、64° D、68°6. 如图,正方形ABCD的顶点A、D分别在x轴、y轴的正半轴上,若反比例函数y= (x>0)的图象经过另外两个顶点B、C,且点B(6,n),(0<n<6),则k的值为( ) A、18 B、12 C、6 D、2
A、18 B、12 C、6 D、2二、填空题
-
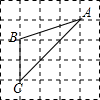
7. 的倒数是.8. 0.0002019用科学记数法可表示为.9. 分解因式:a2b﹣b3= .10. 一元二次方程x2﹣2x=0的两根分别为x1和x2 , 则x1x2为.11. 一个多边形的内角和与外角和之差为720 ,则这个多边形的边数为.12. 已知抛物线y=ax2+bx+c(a>0)的对称轴是直线x=2,且经过点P(3,1),则a+b+c的值为.13. 已知点C为线段AB的黄金分割点,且AC>BC,若P点为线段AB上的任意一点,则P点出现在线段AC上的概率为.14. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为.
 15. 如图,平面直角坐标系中,点A(0,-2),B(-1,0),C(-5,0),点D从点B出发,沿x轴负方向运动到点C,E为AD上方一点,若在运动过程中始终保持△AED~△AOB,则点E运动的路径长为
15. 如图,平面直角坐标系中,点A(0,-2),B(-1,0),C(-5,0),点D从点B出发,沿x轴负方向运动到点C,E为AD上方一点,若在运动过程中始终保持△AED~△AOB,则点E运动的路径长为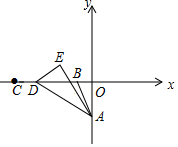
三、解答题
-
16. 计算:17. 解不等式组: .18. 先化简,再求值: ,其中x满足方程x2-2x-3=0.19. 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.
 (1)、求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的基础上,过点P画PE∥AC交BC边于E,联结EQ,则四边形APEQ是什么特殊四边形?证明你的结论.20. 将分别标有数字3,6,9的三张形状、大小均相同的卡片洗匀后,背面朝上放在桌面上.(1)、随机地抽取一张,求抽到数字恰好为6的概率;(2)、随机地抽取张作为十位上的数字(不放回),再抽取一张作为个位上的数字,通过列表或画树状图求所组成的两位数恰好是“69”的概率.21. 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒种后△DPQ的面积为31cm2?
(1)、求作∠ABC的平分线,分别交AD,AC于P,Q两点;(要求:尺规作图,保留作图痕迹,不写作法)(2)、在(1)的基础上,过点P画PE∥AC交BC边于E,联结EQ,则四边形APEQ是什么特殊四边形?证明你的结论.20. 将分别标有数字3,6,9的三张形状、大小均相同的卡片洗匀后,背面朝上放在桌面上.(1)、随机地抽取一张,求抽到数字恰好为6的概率;(2)、随机地抽取张作为十位上的数字(不放回),再抽取一张作为个位上的数字,通过列表或画树状图求所组成的两位数恰好是“69”的概率.21. 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,几秒种后△DPQ的面积为31cm2? 22. 某校开展了为期一周的“新时代文明实践”活动,为了解情况,学生会随机调查了部分学生在这次活动中“宣传文明礼仪”的时间,并将统计的时间(单位:小时)分成5组,A:0.5≤x<1,B;1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).
22. 某校开展了为期一周的“新时代文明实践”活动,为了解情况,学生会随机调查了部分学生在这次活动中“宣传文明礼仪”的时间,并将统计的时间(单位:小时)分成5组,A:0.5≤x<1,B;1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).请根据图中提供的信息,解答下列问题:
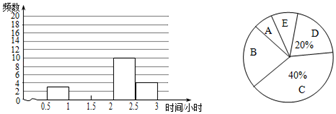 (1)、学生会随机调查了名学生.(2)、补全频数分布直方图.(3)、若全校有900名学生,估计该校在这次活动中“宣传文明礼仪”的时间不少于2小时的学生有多少人?23. 共享单车为大众出行提供了方便,如图为单车实物图,如图为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,∠EAB=45°,车轮半径为0.3m,BE=0.4m.小明体验后觉得当坐垫C离地面高度为0.9m时骑着比较舒适,求此时CE的长.(结果精确到1cm)参考数据:sin70.≈0.94,cos70.≈0.34,tan70.≈2.75, ≈1.41
(1)、学生会随机调查了名学生.(2)、补全频数分布直方图.(3)、若全校有900名学生,估计该校在这次活动中“宣传文明礼仪”的时间不少于2小时的学生有多少人?23. 共享单车为大众出行提供了方便,如图为单车实物图,如图为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知,∠ABE=70°,∠EAB=45°,车轮半径为0.3m,BE=0.4m.小明体验后觉得当坐垫C离地面高度为0.9m时骑着比较舒适,求此时CE的长.(结果精确到1cm)参考数据:sin70.≈0.94,cos70.≈0.34,tan70.≈2.75, ≈1.41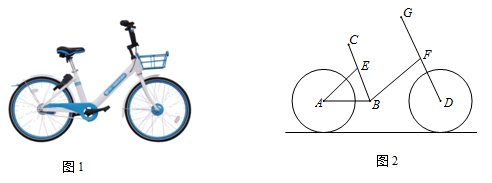 24. 如图,AB,CD是圆O的直径,AE是圆O的弦,且AE∥CD,过点C的圆O切线与EA的延长线交于点P,连接AC.
24. 如图,AB,CD是圆O的直径,AE是圆O的弦,且AE∥CD,过点C的圆O切线与EA的延长线交于点P,连接AC. (1)、求证:AC平分∠BAP;(2)、求证:PC2=PA•PE;(3)、若AE-AP=PC=4,求圆O的半径.25. 如图1,在△ABC中,BA=BC,点D,E分别在边BC、AC上,连接DE,且DE=DC.
(1)、求证:AC平分∠BAP;(2)、求证:PC2=PA•PE;(3)、若AE-AP=PC=4,求圆O的半径.25. 如图1,在△ABC中,BA=BC,点D,E分别在边BC、AC上,连接DE,且DE=DC.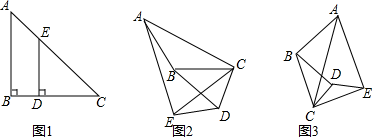 (1)、问题发现:若∠ACB=∠ECD=45°,则 .(2)、拓展探究,若∠ACB=∠ECD=30°,将△EDC绕点C按逆时针方向旋转α度(0°<α<180°),图2是旋转过程中的某一位置,在此过程中 的大小有无变化?如果不变,请求出 的值,如果变化,请说明理由.(3)、问题解决:若∠ACB=∠ECD=β(0°<β<90°),将△EDC旋转到如图3所示的位置时,则 的值为.(用含β的式子表示)26. 如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.
(1)、问题发现:若∠ACB=∠ECD=45°,则 .(2)、拓展探究,若∠ACB=∠ECD=30°,将△EDC绕点C按逆时针方向旋转α度(0°<α<180°),图2是旋转过程中的某一位置,在此过程中 的大小有无变化?如果不变,请求出 的值,如果变化,请说明理由.(3)、问题解决:若∠ACB=∠ECD=β(0°<β<90°),将△EDC旋转到如图3所示的位置时,则 的值为.(用含β的式子表示)26. 如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.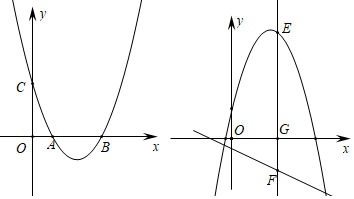 (1)、求抛物线的表达式和顶点D的坐标;(2)、在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;(3)、将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y=- x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.
(1)、求抛物线的表达式和顶点D的坐标;(2)、在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;(3)、将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y=- x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.