江苏省徐州市2019年数学中考三模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- 3$ D、 $3$

查看试题解析
2. 下列计算正确的是（）

A、a²+b³=2a⁵ B、a⁴÷a=a⁴ C、a²•a³=a⁶ D、（﹣a²）³=﹣a⁶

查看试题解析
3. 徐州日报社记者从市铁路运输部门获悉，清明节小长假2019年4月5日至7日期间，徐州铁路运输部门累计发送旅客17.8万人次.用科学记数法表示为（）

A、17.8×10⁵ B、17.8×10⁶ C、1.78×10⁵ D、1.78×10⁶

查看试题解析
4.
一个三棱柱如图所示，它的主视图是（　　）

A、 B、 C、 D、

查看试题解析
5. 等腰三角形底角与顶角之间的函数关系是（）

A、正比例函数 B、一次函数 C、反比例函数 D、二次函数

查看试题解析
6. 下列图形中，既是轴对称图形又是中心对称图形的是 $($ $)$

A、 B、 C、 D、

查看试题解析
7. 如图，若二次函数y=ax²+bx+c（a≠0）图象的对称轴为x=1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则①二次函数的最大值为a+b+c；②a﹣b+c＜0；③b²﹣4ac＜0；④当y＞0时，﹣1＜x＜3，其中正确的个数是（）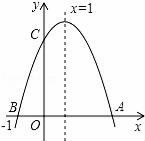

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

8. ﹣ $\frac{1}{2013}$ 的倒数是.

查看试题解析
9. 代数式 $\frac{\sqrt{x - 1}}{x - 2}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
10. 若一个角的余角是它的补角的 $\frac{1}{4}$ ，这个角的度数.

查看试题解析
11. 一个多边形的每个内角都等于150°，则这个多边形是边形．

查看试题解析
12. 若一个圆锥的侧面积是它底面积的2倍，则这个圆锥的侧面展开图的圆心角是．

查看试题解析
13. 如图，在正八边形ABCDEFGH中，连接AC、AE，则 $\frac{A E}{A C}$ ＝.

查看试题解析
14. 若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图像经过点（1，－3），则一次函数y＝kx－k（k≠0）的图像经过象限.

查看试题解析
15. 随看居民经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，抽样调查显示，截止2018年底徐州市汽车拥有量为29.8万辆，已知2016年底该市汽车拥有量为18万辆，设2016年底至2018年底我市汽车拥有量的平均增长率为x，根据题意列方程为.

查看试题解析
16. 如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形.若∠BAD=60°，AB=2，则图中阴影部分的面积为.

查看试题解析
17. 如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G．若图中阴影部分的面积与正方形ABCD的面积之比为2：3，则△BCG的周长为．

查看试题解析

三、解答题

18. 计算
|﹣3|+（﹣1）²⁰¹⁹﹣（1﹣ $\sqrt{3})$ ⁰﹣2sin60°

查看试题解析
19.

(1)、解方程：x²﹣2x﹣1＝0；

(2)、解不等式组： ${\begin{matrix} 3 x + 1 < 2 x + 3 \\ 2 x > \frac{3 x - 1}{2} \end{matrix}$

查看试题解析
20. 目前我市“校园手机”现象越来越受到社会关注，针对这种现象，随机抽查了某中学九年级的同学，关于手机在中学生中的主要用途做了调查，对调查数据进行统计整理、制作了如下的两种统计图：请根据图形回答问题

(1)、这次被调查的学生共有人，其中主要用于“上网聊天”的学生人数占抽样人数的百分比为；

(2)、请你将条形统计图（2）补充完整；

(3)、若该校共有3000名学生，请你估计主要使用手机玩游戏的人数大约有多少人？

查看试题解析
21. 已知：如图，在菱形 $A B C D$ 中，点 $E$ ， $O$ ， $F$ 分别为 $A B$ ， $A C$ ， $A D$ 的中点，连接 $C E$ ， $C F$ ， $O E$ ， $O F$ .

(1)、求证： $△ B C E ≅ △ D C F$ ；

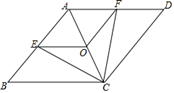(2)、当 $A B$ 与 $B C$ 满足什么关系时，四边形 $A E O F$ 是正方形？请说明理由.

查看试题解析
22. “低碳生活，绿色出行”的理念已深入人心，现在越来越多的人选择骑自行车上下班或外出旅游.周末，小红相约到郊外游玩，她从家出发0.5小时后到达甲地，玩一段时间后按原速前往乙地，刚到达乙地，接到妈妈电话，快速返回家中.小红从家出发到返回家中，行进路程y（km）随时间x（h）变化的函数图象大致如图所示.

(1)、小红从甲地到乙地骑车的速度为km/h；

(2)、当1.5≤x≤2.5时，求出路程y（km）关于时间x（h）的函数解析式；并求乙地离小红家多少千米？

查看试题解析
23. 如图，C是⊙O上一点，点P在直径AB的延长线上，⊙O的半径为3，PB=2，PC=4．

(1)、求证：PC是⊙O的切线．

(2)、求tan∠CAB的值．

查看试题解析
24. 某新农村乐园设置了一个秋千场所，如图所示，秋千拉绳OB的长为3m，静止时，踏板到地面距离BD的长为0.6m（踏板厚度忽略不计）.为安全起见，乐园管理处规定：儿童的“安全高度”为hm，成人的“安全高度”为2m（计算结果精确到0.1m）

（参考数据： $\sqrt{2}$ ≈1.41，sin55°≈0.82，cos55°≈0.57，tan55°≈1.43）

(1)、当摆绳OA与OB成45°夹角时，恰为儿童的安全高度，则h＝m

(2)、某成人在玩秋千时，摆绳OC与OB的最大夹角为55°，问此人是否安全？

查看试题解析
25. 在△ABC中，∠ACB=2∠B，如图①，当∠C=90°，AD为∠BAC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD.

(1)、如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想：

(2)、如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明.

查看试题解析
26. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} + b x + c$ 交 $x$ 轴于点 $A (- 4 ， 0)$ 、 $B (2 ， 0)$ ，交 $y$ 轴于点 $C (0 ， 6)$ ，在 $y$ 轴上有一点 $E (0 ， - 2)$ ，连接 $A E$ .

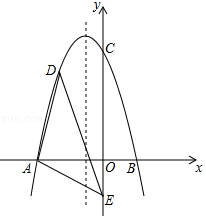(1)、求二次函数的表达式；

(2)、若点 $D$ 为抛物线在 $x$ 轴负半轴上方的一个动点，求 $Δ A D E$ 面积的最大值；

(3)、抛物线对称轴上是否存在点 $P$ ，使 $Δ A E P$ 为等腰三角形，若存在，请直接写出所有 $P$ 点的坐标，若不存在请说明理由.

查看试题解析