江苏省宿迁市2019届初中毕业暨升学模拟数学试卷（6月）

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{1}{3}$ 的相反数是（）

A、3 B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、﹣3

查看试题解析
2. 一个整数8150…0用科学记数法表示为8.15×10¹⁰ ，则原数中“0”的个数为（）

A、7 B、8 C、9 D、10

查看试题解析
3. 下列计算正确的是（）

A、a²﹣5a²＝﹣5 B、(﹣a²)³＝a⁶ C、2a+b＝2ab D、a²•a⁴＝a⁶

查看试题解析
4. 有一组数据：1，2，2，5，6，8，这组数据的中位数是（）

A、2 B、2.5 C、3.5 D、5

查看试题解析
5. 一个正多边形的每一个外角都等于45°，则这个多边形的边数为（）

A、4 B、6 C、8 D、10

查看试题解析
6. 如图，在边长为1的小正方形网格中，△ABC的三个顶点均在格点上，若向正方形网格中投针，落在△ABC内部的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{3}{8}$ D、 $\frac{5}{16}$

查看试题解析
7. 如图，△ABC是等边三角形，点C在直线b上，若直线a∥b，∠1＝34°，则∠2的度数为（）

A、26° B、28° C、34° D、36°

查看试题解析
8. 若2019个数a₁、a₂、a₃、…、a₂₀₁₉满足下列条件：a₁＝2，a₂＝﹣|a₁+5|，a₃＝﹣|a₂+5|，…，a₂₀₁₉＝﹣|a₂₀₁₈+5|，则a₁+a₂+a₃+…+a₂₀₁₉＝（）

A、﹣5040 B、﹣5045 C、﹣5047 D、﹣5051

查看试题解析

二、填空题

9. 已知∠A＝60°，则cosA＝.

查看试题解析
10. 函数y＝ $\sqrt{x-1}$ 的自变量x的取值范围是.

查看试题解析
11. 已知 ${\begin{array}{l} x = m \\ y = n \end{array}$ 是方程组 ${\begin{array}{l} x - 2 y = 0 \\ 2 x + 3 y = 4 \end{array}$ 的解，则3m+n＝.

查看试题解析
12. 二次函数y＝﹣x²+2x图象的顶点坐标是.

查看试题解析
13. 如图⊙O中，直径AB⊥弦CD于E，若AB＝26，CD＝24，则tan∠OCE＝.

查看试题解析
14. 设α，β是方程x²﹣x﹣2019＝0的两个实数根，则α²+β的值为.

查看试题解析
15. 如图，△ABC内接于⊙O，∠OAC＝25°，则∠ABC＝.

查看试题解析
16. 如果一个函数的图象关于y轴成轴对称图形，那么我们把这个函数叫做偶函数，则下列5个函数：①y＝﹣3x﹣1，② $y = \frac{6}{x}$ ，③y＝x²+1，④y＝﹣|x|，⑤ $y = \frac{x}{x^{2} + 1}$ 中的偶函数是(填序号).

查看试题解析
17. 若min{a，b，c}表示a，b，c三个数中的最小值，当y＝min{x² ， x+2，8﹣x}(x≥0)时，则y的最大值是.

查看试题解析

三、解答题

18. 计算： $4 \sin 45 ° - \sqrt{18} - | 2 - \sqrt{2} | - {(- \frac{1}{2})}^{- 2}$ .

查看试题解析
19. 解不等式组 ${\begin{array}{l} 2 x - 4 \geq 3 (x - 2) \\ 4 x > \frac{x - 7}{2} \end{array}$ .

查看试题解析
20. 在“弘扬传统文化，打造书香校园”的活动中，学校计划开展四项活动：“A﹣国学诵读”，“B﹣演讲”，“C﹣课本剧”，“D﹣书法”，要求每位同学必须且只能参加其中一项活动，学校为了了解学生的意愿，随机调查了部分学生，结果统计如图：

(1)、如图，则被调查的总人数为人；扇形统计图中，希望参加活动A所占圆心角为度.

(2)、根据题中信息补全条形统计图；

(3)、学校现有1000名学生，请根据图中信息，估算全校学生希望参加活动D有多少人？

查看试题解析
21. 有4张正面分别标有数字﹣1，2，﹣3，4的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上，洗匀后从4张卡片中随机摸出一张不放回，将该卡片上的数字记为m，再随机抽取1张，将卡片的数字记为n.

(1)、请用列表或树状图的方式把(m，n)所有的结果表示出来.

(2)、求选出的(m，n)在一、三象限的概率.

查看试题解析
22. 如图，在四边形 $A B C D$ 中， $A B ∥ D C$ ， $A B = A D$ ，对角线 $A C$ ， $B D$ 交于点 $O$ ， $A C$ 平分 $∠ B A D$ ，过点 $C$ 作 $C E ⊥ A B$ 交 $A B$ 的延长线于点 $E$ ，连接 $O E$ .

(1)、求证：四边形 $A B C D$ 是菱形；

(2)、若 $A B = \sqrt{5}$ ， $B D = 2$ ，求 $O E$ 的长.

查看试题解析
23. 如图，MN为一电视塔，AB是坡角为30°的小山坡(电视塔的底部N与山坡的坡脚A在同一水平线上，被一个人工湖隔开)，某数学兴趣小组准备测量这座电视塔的高度.在坡脚A处测得塔顶M的仰角为45°；沿着山坡向上行走40m到达C处，此时测得塔顶M的仰角为30°，请求出电视塔MN的高度.(参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73，结果保留整数)

查看试题解析

24. 我市某工艺厂，设计了一款成本为20元/件的工艺品投放市场进行试销，经过市场调查，得到如下数据：

销售单价x(元∕件)	…	30	40	50	60	…
每天销售量y(件)	…	500	400	300	200	…

(1)、上表中x、y的各组对应值满足一次函数关系，请求出y与x的函数关系式；

(2)、物价部门规定，该工艺品销售单价最高不能超过45元/件，那么销售单价定为多少时，工艺厂试销该工艺品每天获得的利润最大？最大利润是多少？

查看试题解析

25. 如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作AE⊥CD，交CD的延长线于点E，DA平分∠BDE.

(1)、求证：AE是⊙O的切线；

(2)、已知AE＝8cm，CD＝12cm，求⊙O的半径.

查看试题解析
26. 如图，抛物线y＝﹣ $\frac{1}{2}$ x²+bx+c与x轴交于A、B两点，直线y＝ $\frac{1}{2}$ x+ $\frac{1}{2}$ 经过点A，与抛物线的另一个交点为点C(3，m)，线段PQ在线段AB上移动，PQ＝1，分别过点P、Q作x轴的垂线，交抛物线于E、F，交直线于D、G.

(1)、求抛物线的解析式；

(2)、设四边形DEFG的面积为S，求S的最大值；

(3)、在线段PQ的移动过程中，以D，E，F，G为顶点的四边形是平行四边形时，求点P的坐标.

查看试题解析
27. 在平面直角坐标系xOy中，⊙C的半径为r(r＞1)，点P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：过圆心C的任意直线CP与⊙C交于点A，B，若满足|PA﹣PB|＝2，则称点P为⊙C的“完美点”，如图点P为⊙C的一个“完美点”.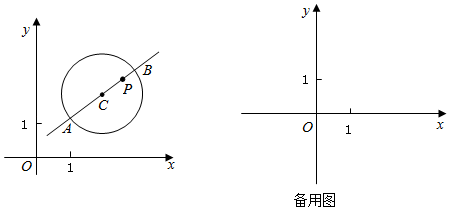

(1)、当⊙O的半径为2时
①点M( $\frac{3}{2}$ ，0)⊙O的“完美点”，点(﹣ $\frac{\sqrt{3}}{2}$ ，﹣ $\frac{1}{2}$ )⊙O的“完美点”；(填“是”或者“不是”)
②若⊙O的“完美点”P在直线y＝ $\frac{3}{4}$ x上，求PO的长及点P的坐标；

(2)、设圆心C的坐标为(s，t)，且在直线y＝﹣2x+1上，⊙C半径为r，若y轴上存在⊙C的“完美点”，求t的取值范围.

查看试题解析