贵州省遵义市汇川区2019届九年级第二次中考适应性考试数学试卷
试卷更新日期:2020-01-09 类型:中考模拟
一、单选题
-
1. – 的倒数是( )A、–5 B、5 C、– D、2. 下列图形中,既是轴对称图形又是中心对称图形的是A、
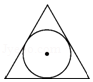 B、
B、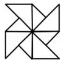 C、
C、 D、
D、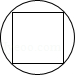 3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图形中,由 ,能得到 的是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 下列图形中,由 ,能得到 的是( )A、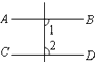 B、
B、 C、
C、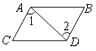 D、
D、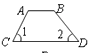 5. 在平面直角坐标系中,若点P(m﹣2,m+1)在第二象限,则m的取值范围是( )A、m<﹣1 B、m>2 C、﹣1<m<2 D、m>﹣16. 陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
5. 在平面直角坐标系中,若点P(m﹣2,m+1)在第二象限,则m的取值范围是( )A、m<﹣1 B、m>2 C、﹣1<m<2 D、m>﹣16. 陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( ) A、19 B、18 C、16 D、157. 为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
A、19 B、18 C、16 D、157. 为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )捐款数额
10
20
30
50
100
人数
2
4
5
3
1
A、众数是100 B、中位数是30 C、极差是20 D、平均数是308. 下列函数中,自变量x的取值范围为x>1的是( )A、 B、 C、 D、y=(x﹣1)09. 如图所示,已知 中, , 边上的高 , 为 上一点, ,交 于点 ,交 于点 ,设点 到边 的距离为 .则 的面积 关于 的函数图象大致为( )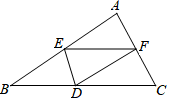 A、
A、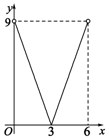 B、
B、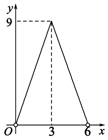 C、
C、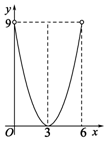 D、
D、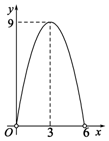 10. 如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )
10. 如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于点F,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )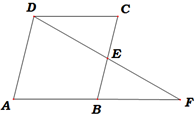 A、AD=BC B、CD=BF C、∠A=∠C D、∠F=∠CDE11. 尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
A、AD=BC B、CD=BF C、∠A=∠C D、∠F=∠CDE11. 尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?大臣给出的正确答案应是( )
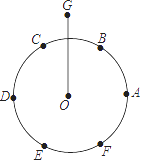 A、 r B、(1+ )r C、(1+ )r D、 r12. 如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱ALMN,若中间空白部分四边形OPQR恰好是正方形,且▱ALMN的面积为50,则正方形EFGH的面积为( )
A、 r B、(1+ )r C、(1+ )r D、 r12. 如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的▱ALMN,若中间空白部分四边形OPQR恰好是正方形,且▱ALMN的面积为50,则正方形EFGH的面积为( )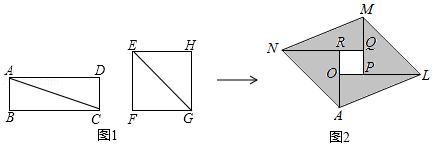 A、24 B、25 C、26 D、27
A、24 B、25 C、26 D、27二、填空题
-
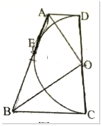
13. 不透明的布袋里有1个黄球、4个红球、5个白球,它们除颜色外其他都相同,那么从布袋中任意摸出一球恰好为红球的概率是.14. 已知m+n=12,m-n=2,则m2-n2=.15. 如图,已知半圆 与四边形 的边 都相切,切点分别为 ,半径 ,则 .
 16. 在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),M为BC中点,反比例函数 (k是常数,k≠0) 的图象经过点M,交AC于点N,则MN的长度是.
16. 在平面直角坐标系中,四边形AOBC为矩形,且点C坐标为(8,6),M为BC中点,反比例函数 (k是常数,k≠0) 的图象经过点M,交AC于点N,则MN的长度是.
三、解答题
-
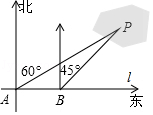
17. 计算:(1)、(2)、18. 先化简,再求值 ,其中 .19. 为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据: ≈1.414, ≈1.732)
 20. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
20. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):步数
频数
频率
0≤x<4000
8
a
4000≤x<8000
15
0.3
8000≤x<12000
12
b
12000≤x<16000
c
0.2
16000≤x<20000
3
0.06
20000≤x<24000
d
0.04
请根据以上信息,解答下列问题:
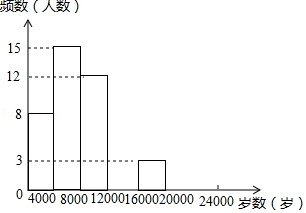 (1)、写出a,b,c,d的值并补全频数分布直方图;(2)、本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?(3)、若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.21. 如图,在 中, , ,点 在 上,经过点 的 与 相切于点 ,交 于点 .
(1)、写出a,b,c,d的值并补全频数分布直方图;(2)、本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?(3)、若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.21. 如图,在 中, , ,点 在 上,经过点 的 与 相切于点 ,交 于点 . (1)、求证: 平分 ;(2)、若 ,求图中阴影部分的面积(结果保留 ).22. “绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:
(1)、求证: 平分 ;(2)、若 ,求图中阴影部分的面积(结果保留 ).22. “绿水青山就是金山银山”,为了保护环境和提高果树产量,某果农计划从甲、乙两个仓库用汽车向A,B两个果园运送有机化肥,甲、乙两个仓库分别可运出80吨和100吨有机化肥;A,B两个果园分别需用110吨和70吨有机化肥.两个仓库到A,B两个果园的路程如表所示:路程(千米)
甲仓库
乙仓库
A果园
15
25
B果园
20
20
设甲仓库运往A果园x吨有机化肥,若汽车每吨每千米的运费为2元,
(1)、根据题意,填写下表.(温馨提示:请填写在答题卷相对应的表格内)运量(吨)
运费(元)
甲仓库
乙仓库
甲仓库
乙仓库
A果园
x
110﹣x
2×15x
2×25(110﹣x)
B果园
(2)、设总运费为y元,求y关于x的函数表达式,并求当甲仓库运往A果园多少吨有机化肥时,总运费最省?最省的总运费是多少元?23. 如图,已知直线 分别交 轴、 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC 轴于点C,交抛物线于点D.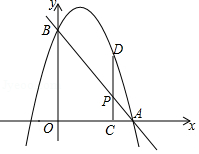 (1)、若抛物线的解析式为 ,设其顶点为M,其对称轴交AB于点N.
(1)、若抛物线的解析式为 ,设其顶点为M,其对称轴交AB于点N.①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)、当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与 AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.24. 如图,在平面直角坐标系中,一次函数y=﹣ x+4的图象与x轴和y轴分别相交于A、B两点.动点P从点A出发,在线段AO上以每秒3个单位长度的速度向点O作匀速运动,到达点O停止运动,点A关于点P的对称点为点Q,以线段PQ为边向上作正方形PQMN.设运动时间为t秒. (1)、当t= 秒时,点Q的坐标是;(2)、在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)、若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.
(1)、当t= 秒时,点Q的坐标是;(2)、在运动过程中,设正方形PQMN与△AOB重叠部分的面积为S,求S与t的函数表达式;(3)、若正方形PQMN对角线的交点为T,请直接写出在运动过程中OT+PT的最小值.