甘肃省张掖市高台县2019届数学中考二模试卷

试卷更新日期：2020-01-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算结果等于x³的是（）

A、x⁶÷x² B、x⁴﹣x C、x+x² D、x²•x

查看试题解析
2. 某种零件模型可以看成如图所示的几何体(空心圆柱)，该几何体的俯视图是（）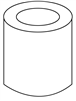

A、 B、 C、 D、

查看试题解析
3. 如图，已知AB∥DE，∠ABC＝75°，∠CDE＝145°，则∠BCD的值为（）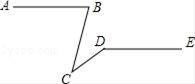

A、20° B、30° C、40° D、70°

查看试题解析
4. 下列计算正确的是（）

A、x²+x²=x⁴ B、x⁸÷x²=x⁴ C、x²•x³=x⁶ D、（-x）²-x²=0

查看试题解析
5. 关于x的一元二次方程x²+4x+k=0有两个实数根，则k的取值范围是（）

A、k≤﹣4 B、k＜﹣4 C、k≤4 D、k＜4

查看试题解析
6. 如图，在△ABC中，∠C＝35°，以点A，C为圆心，大于 $\frac{1}{2}$ AC长为半径画弧交于点M，N，作直线MN，交BC于点D，连接AD，∠BAD＝60°，则∠ABC的度数为（）

A、50° B、65° C、55° D、60°

查看试题解析
7. 如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m² ．若设道路的宽为xm，则下面所列方程正确的是（）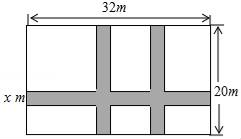

A、（32﹣2x）（20﹣x）=570 B、32x+2×20x=32×20﹣570 C、（32﹣x）（20﹣x）=32×20﹣570 D、32x+2×20x﹣2x²=570

查看试题解析
8. 如图所示，菱形ABCD中，对角线AC、BD相交于点O，H为AD边的中点，菱形ABCD的周长为36，则OH的长等于（）

A、4.5 B、5 C、6 D、9

查看试题解析
9. 如图，已知直线 $y_{1} = k_{1} x + m$ 和直线 $y_{2} = k_{2} x + n$ 交于点 $P (- 1 ， 2)$ ，则关于x的不等式 $(k_{1} - k_{2}) x > - m + n$ 的解是（）

A、 $x > 2$ B、 $x > - 1$ C、 $- 1 < x < 2$ D、 $x < - 1$

查看试题解析
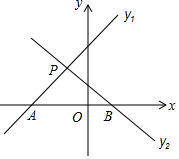10. 如图，AB与⊙O相切于点C，OA＝OB，⊙O的直径为6cm，AB＝6 $\sqrt{3}$ cm，则阴影部分的面积为（）

A、 $(9 \sqrt{3} - π) {cm}^{2}$ B、 $(9 \sqrt{3} - 2 π) {cm}^{2}$ C、 $(9 \sqrt{3} - 3 π) {cm}^{2}$ D、 $(9 \sqrt{3} - 4 π) {cm}^{2}$

查看试题解析

二、填空题

11. 若使代数式 $\frac{2 x - 1}{x + 2}$ 有意义，则x的取值范围是.

查看试题解析
12. 已知两个角的和是67°56′，差是12°40′，则这两个角的度数分别是.

查看试题解析
13. 已知菱形的周长为20cm，一条对角线长为6cm，则这个菱形的面积是cm².

查看试题解析
14. 如图，△ABC内接于⊙O，若∠OAB=32°，则∠C=°．

查看试题解析
15. 有七张正面分别标有数字﹣1、﹣2、0、1、2、3、4的卡片，除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为m，则使关于x的方程x²﹣2（m﹣1）x+m²﹣3m＝0有实数根，且不等式组 ${\begin{array}{l} 2 x + 3 > 9 \\ x - m < 0 \end{array}$ 无解的概率是.

查看试题解析
16. 抛物线 y= -x $^{2}$ + bx + c 的部分图象如图所示，则关于 x 的一元二次方程-x $^{2}$ + bx + c= 0 的解为

查看试题解析
17. 如图，在△ABC中，∠ACB＝90°，AC＝1，AB＝2，以点A为圆心、AC的长为半径画弧，交AB边于点D，则弧CD的长等于.（结果保留π）

查看试题解析

三、解答题

18.

(1)、计算： $4 \sin 60^{°} - | - 1 | + {(\sqrt{3} - 1)}^{0} + \sqrt{48}$ ；

(2)、解不等式组 ${\begin{array}{l} \frac{1}{2} (x - 1) ⩽ 1 \\ 1 - x < 2 \end{array}$ ，并写出该不等式组的最大整数解.

查看试题解析
19. 如图，已知△ABC，请用圆规和直尺作出△ABC的一条中位线EF（不写作法，保留作图痕迹）.

查看试题解析
20. 如图，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得点C的仰角为45°，已知OA＝100米，山坡坡度(竖直高度与水平宽度的比)i＝1：2，且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计，结果保留根号形式)

查看试题解析
21. 如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F.

(1)、求证：四边形BEDF是平行四边形；

(2)、当四边形BEDF是菱形时，求EF的长.

查看试题解析
22. 某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计，并绘制如图所示的扇形统计图和条形统计图．根据图中信息解答下列问题：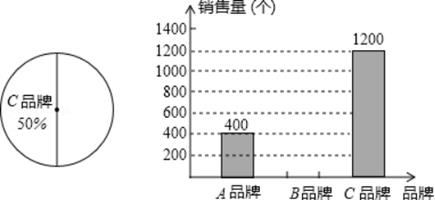

(1)、该超市“元旦”期间共销售个绿色鸡蛋，A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是度；

(2)、补全条形统计图；

(3)、如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个，请你估计这个分店销售的B种品牌的绿色鸡蛋的个数？

查看试题解析
23. 如图，在平面直角坐标系xOy中，已知正比例函数y₁＝﹣2x的图象与反比例函数y₂＝ $\frac{k}{x}$ 的图象交于A（﹣1，n），B两点.

(1)、求出反比例函数的解析式及点B的坐标；

(2)、观察图象，请直接写出满足y≤2的取值范围；

(3)、点P是第四象限内反比例函数的图象上一点，若△POB的面积为1，请直接写出点P的横坐标.

查看试题解析
24. 如图，O为菱形ABCD对角线上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点M.

(1)、求证：CD与⊙O相切；

(2)、若菱形ABCD的边长为2，∠ABC＝60°，求⊙O的半径.

查看试题解析
25. 某商场一种商品的进价为每件 30 元，售价为每件 40 元，每天可以销售 48 件，为尽快减少库存，商场决定降价促销．

(1)、若该商品连续两次下调相同的百分率后售价降至每件 32.4 元，求两次下降的百分率；

(2)、经调查，若该商品每降价 0.5 元，每天可多销售 4 件，那么每天要想获得 510 元的利润，每件应降价多少元？

查看试题解析
26. 如图，已知二次函数y＝ax²＋bx＋4的图象与x轴交于点B(－2，0)，点C(8，0)，与y轴交于点A.

(1)、求抛物线的解析式；

(2)、连接AC，AB，若点N在线段BC上运动(不与点B，C重合)，过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求N点的坐标；

(3)、连接OM，在(2)的结论下，求OM与AC的数量关系.

查看试题解析