甘肃省金昌市2019届数学中考二模试卷
试卷更新日期:2020-01-09 类型:中考模拟
一、单选题
-
1. -5的相反数是( )A、-5 B、5 C、 D、2. 据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )A、0.3×106 B、3×105 C、3×106 D、30×1043. 下列计算正确的是( )A、a3•a2=a6 B、(a3)2=a5 C、(ab2)3=ab6 D、a+2a=3a4.
下列美丽的图案中,既是轴对称图形又是中心对称图形的个数有( )
 A、1个 B、2个 C、3个 D、4个5. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )
A、1个 B、2个 C、3个 D、4个5. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是( )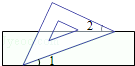 A、15° B、20° C、25° D、30°6. 一元二次方程x2+x﹣2=0根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定7. 分式方程 = 的解是( )
A、15° B、20° C、25° D、30°6. 一元二次方程x2+x﹣2=0根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定7. 分式方程 = 的解是( )
A、x=1 B、x=﹣1 C、x=3 D、x=﹣38. 某超市一月份的营业额为36万元,三月份的营业额为48万元,设每月的平均增长率为x,则可列方程为( )A、48(1﹣x)2=36 B、48(1+x)2=36 C、36(1﹣x)2=48 D、36(1+x)2=489. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,
错误的个数有( )
 A、1个 B、2个 C、3个 D、4个10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )
A、1个 B、2个 C、3个 D、4个10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )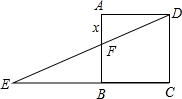 A、
A、 B、
B、 C、
C、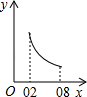 D、
D、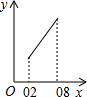
二、填空题
-
11. 分解因式:x2y﹣4y= .12. 不等式2x+9≥3(x+2)的正整数解是13. 函数y= 的自变量x的取值范围是 .14. 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O)20米的A处,则小明的影子AM长为米.
 15. 如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B=.
15. 如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B=. 16. 如图,△ABC中,DE∥BC, ,△ADE的面积为8,则△ABC的面积为
16. 如图,△ABC中,DE∥BC, ,△ADE的面积为8,则△ABC的面积为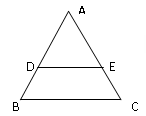 17. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于 的二元一次方程组的解是.
17. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于 的二元一次方程组的解是. 18. 现定义运算“★”,对于任意实数a、b,都有a★b=a2﹣3a+b,如:3★5=32﹣3×3+5,若x★2=6,则实数x的值是 .
18. 现定义运算“★”,对于任意实数a、b,都有a★b=a2﹣3a+b,如:3★5=32﹣3×3+5,若x★2=6,则实数x的值是 .三、解答题
-
19. 计算: .20. 先化简,再求值: ÷(m﹣1﹣ ),其中m= .21. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
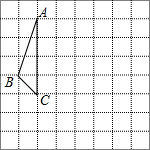 (1)、画出△ABC绕点C顺时针旋转90°后的△A1B1C;(2)、求边AC旋转时所扫过区域的面积.22. 如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(1)、画出△ABC绕点C顺时针旋转90°后的△A1B1C;(2)、求边AC旋转时所扫过区域的面积.22. 如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据: ≈1.732)
 23. 已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2),
23. 已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,﹣2), (1)、求这两个函数的关系式;(2)、观察图象,写出使得y1>y2成立的自变量x的取值范围;(3)、如果点C与点A关于x轴对称,求△ABC的面积.24. 如图,袋子里装有4个球,大小形状完全一样,上面分别标有 ,0,﹣π, ,从中任意取2个球.
(1)、求这两个函数的关系式;(2)、观察图象,写出使得y1>y2成立的自变量x的取值范围;(3)、如果点C与点A关于x轴对称,求△ABC的面积.24. 如图,袋子里装有4个球,大小形状完全一样,上面分别标有 ,0,﹣π, ,从中任意取2个球. (1)、用树状图或列表法列出所有可能的结果(请用字母A、B、C、D表示)(2)、求取到的2个球上的数字都是有理数的概率.25. 学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)、用树状图或列表法列出所有可能的结果(请用字母A、B、C、D表示)(2)、求取到的2个球上的数字都是有理数的概率.25. 学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题: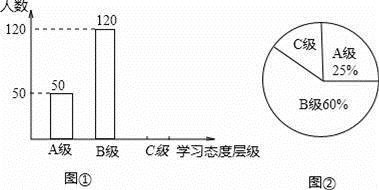 (1)、此次抽样调查中,共调查了名学生;(2)、将图①补充完整;(3)、求出图②中C级所占的圆心角的度数;(4)、根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?26. 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
(1)、此次抽样调查中,共调查了名学生;(2)、将图①补充完整;(3)、求出图②中C级所占的圆心角的度数;(4)、根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?26. 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.
 27. 如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
27. 如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC. (1)、求证:EF是⊙O的切线;(2)、求证:AC2=AD•AB.28. 如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.
(1)、求证:EF是⊙O的切线;(2)、求证:AC2=AD•AB.28. 如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.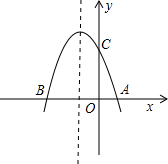 (1)、求该抛物线的解析式;(2)、设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)、在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
(1)、求该抛物线的解析式;(2)、设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;(3)、在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.