辽宁省鞍山市2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2020-01-09 类型：期末考试

进入出卷网下载

一、单选题

1. 一5的绝对值是（）

A、5 B、 $\frac{1}{5}$ C、 $- \frac{1}{5}$ D、－5

查看试题解析
2. 十九大报告指出：“我国经济保持中高速增长，在世界主要国家中名列前茅，国内生产总值从五十四万亿元增长到八十万亿元，稳居世界第二”，其中八十万亿元用科学记数法表示为（）

A、 $0.8 \times 10^{14}$ B、 $8 \times 10^{13}$ C、 $8 \times 10^{12}$ D、 $0.8 \times 10^{13}$

查看试题解析
3. 已知代数式 $- 3 a^{m - 1} b^{6}$ 和 $\frac{1}{6} {ab}^{2 n}$ 是同类项，则m-n的值是（）

A、-1 B、-2 C、-3 D、0

查看试题解析
4. 下列说法中：①一个有理数不是正数就是负数；②射线AB和射线BA是同一条射线；③0的相反数是它本身；④两点之间，线段最短，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 某书店把一本书按进价提高60%标价，再按七折出售，这样每卖出一本书就可赢利6元.设每本书的进价是x元，根据题意列一元一次方程，正确的是（）

A、 $(1 + 60 %) x \cdot \frac{7}{10} = 6$ B、 $60 % x \cdot \frac{7}{10} - x = 6$ C、 $(1 + 60 %) x \cdot \frac{7}{10} - x = 6$ D、 $(1 + 60 %) x - x = 6$

查看试题解析
6. 已用点A，B，C，D，E的位置如图所示，下列结论中正确的是（）

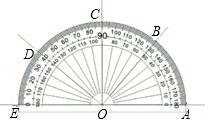A、∠AOB＝130° B、∠AOB＝∠DOE C、∠DOC与∠BOE互补 D、∠AOB与∠COD互余

查看试题解析
7. 已知线段 $A B = 6$ ，在直线AB上取一点C，使 $B C = 2$ ，则线段AC的长（）

A、2 B、4 C、8 D、8或4

查看试题解析
8. 实数a、b、c在数轴上的位置如图所示，则代数式|c﹣a|﹣|a+b|的值等于（）

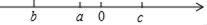A、c+b B、b﹣c C、c﹣2a+b D、c﹣2a﹣b

查看试题解析

二、填空题

9. $| - \frac{1}{2} |$ 的相反数为.

查看试题解析
10. 请写出一个单项式，同时满足下列条件：①含有字母m、n：②系数是负整数；③次数是3，你写的单项式为.

查看试题解析
11. 如图，在正方形网格中，点O、A、B、C、D均是格点.若OE平分∠BOC，则∠DOE的度数为°.

查看试题解析
12. 已知 $| x + 1 | + （ 3 - y ）^{2} = 0$ ，则x $^{y}$ 的值是.

查看试题解析
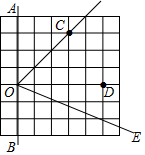13. 已知a+b＝2，则多项式2﹣3a﹣3b的值是.

查看试题解析
14. 若一个角比它的补角大36°48＇，则这个角为°＇.

查看试题解析
15. 甲组有33个人，乙组有27个人，从乙组调若干人到甲组后，甲组的人数恰好是乙组的3倍，求变化后乙组有人.

查看试题解析
16. 有一列数 4，7，x₃ ， x₄ ， …，x_n ，从第二个数起，每一个数都是它前一个数和后一个数和的一半，则当 n≥2 时， $x_{n}$ ＝.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 2^{2} + 8 \div (- 2) \times \frac{1}{4} - {(- 1)}^{2019}$

(2)、 $- \frac{3}{2} \times [- 3^{2} \times {(- \frac{2}{3})}^{2} - 2]$ .

查看试题解析
18. 解方程： $x - \frac{x - 1}{4} = 1 - \frac{3 - x}{2}$

查看试题解析
19. 先化简，再求值： $3 x^{2} y - [2 x^{2} y - x （ x y + 3 ）]$ ，其中 $x = - \frac{1}{2}$ ，y=2.

查看试题解析
20. 已知多项式A、B，其中 $A = x^{2} + 2 x - 1$ ，某同学在计算A+B时，由于粗心把A+B看成了A-B求得结果为 $- 3 x^{2} + 2 x - 1$ ，请你算出A+B的正确结果。

查看试题解析
21. 如图，N为线段AC中点，点M、点B分别为线段AN、NC上的点，且满足 $A M ： M B ： B C = 1 ： 4 ： 3$ .

(1)、若 $A N = 6$ ，求AM的长；

(2)、若 $N B = 2$ ，求AC的长.

查看试题解析
22. 已知：如图，直线AB、CD相交于点O，OE⊥OC，OF平分∠AOE.

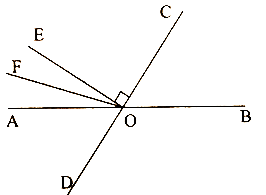(1)、若 $∠ B O C = 60 °$ ，则∠AOF的度数为；

(2)、若 $∠ C O F = x °$ ，求∠BOC的度数。

查看试题解析
23. 上海到北京的G102次列车平均每小时行驶200公里，每天6：30发车，从北京到上海的G5次列车平均每小时行驶280公里，每天7：00发车，已知北京到上海高铁线路长约1180公里，问两车几点相遇？

查看试题解析
24. 某商场购进西装30件，衬衫45件，共用了39000元，其中西装的单价是衬衫的5倍。

(1)、求西装和衬衫的单价各为多少元？

(2)、商场仍需要购买上面的两种产品55件（每种产品的单价不变），采购部预算共支出32000元，财会算了一下，说：“如果你用这些钱共买这两种产品，那么账肯定算错了”请你用学过的方程知识解释财会为什么会这样说？

查看试题解析
25. 如图1，点O为直线AB上一点，过O点作射线OC，使 $∠ A O C ： ∠ B O C = 1 ： 3$ ，将一直角三角板的直角顶点放在点O处，一边ON在射线OA上，另一边OM在直线AB的下方。

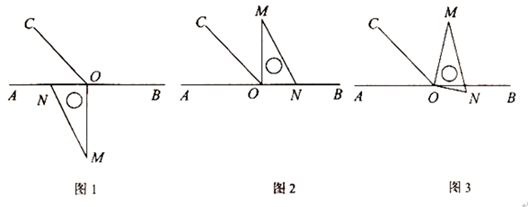(1)、将图1中的三角板绕点O按逆时针方向旋转至图2的位置，使得ON落在射线OB上，此时三角板旋转的角度为度；

(2)、在（1）旋转过程中，当旋转至图3的位置时，使得OM在∠BOC的内部，ON落在直线AB下方，试探究∠COM与∠BON之间满足什么等量关系，并说明理由.

查看试题解析