江苏省扬州市宝应县2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. 如表记录的是今年宝应入冬以来连续四周的平均气温，请问周平均气温最低的是（）

记录周次

第一周

第二周

第三周

第四周

平均气温

3℃

0℃

-5℃

-2℃

A、第一周 B、第二周 C、第三周 D、第四周

查看试题解析
2. 下列运算正确的是（）

A、 $| - 3 | = 3$ B、 $- (- 3) = - 3$ C、 $3 ab + 2 ab = 5 a^{2} b^{2}$ D、 $- 2 a^{3} b + 4 a^{3} b = - 6 a^{3} b$

查看试题解析
3. 如下左图的几何体是由一个圆柱体和一个长方体组成的，则这个几何体的俯视图是（）.

A、 B、 C、 D、

查看试题解析
4. 小明经销一种服装，进货价为每件a元，经测算先将进货价提高200%进行标价，春节前夕又按标价的4折销，这件服装的实际价格是（）

A、 $40 % (a + 200 %)$ 元 B、 $(1 + 200 %) a \times 40 %$ 元 C、 $(a + 200 % - 40 %)$ 元 D、 $(1 + 200 % - 40 %) a$ 元

查看试题解析
5. 下列多项式是五次多项式的是（）

A、 $x^{3} + y^{2}$ B、 $x^{2} y^{3} + xy + 4$ C、 $x^{5} y - l$ D、 $x^{5} - y^{6} + 1$

查看试题解析
6. 如图，OA⊥OB，OC⊥OD，若∠1=50°，则∠2的度数是（）

A、 $20^{\circ}$ B、 $40^{\circ}$ C、 $50^{\circ}$ D、 $60^{\circ}$

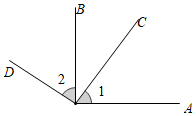查看试题解析
7. 在如图的2018年12月份的月历表中，任意框出表中竖列上三个相邻的数，这三个数的和不可能是（）

A、27 B、51 C、69 D、75

查看试题解析
8. 已知实数a，b在数轴上对应的点如图所示，则下列式子正确的是（）

A、 $- a < - b$ B、 $a + b < 0$ C、 $| a | < | b |$ D、 $a - b > 0$

查看试题解析

二、填空题

9. 为提高全民健康意识，2018年11月25日共青团宝应县委继续组织了一次万人参加的“全民健康行”毅行活动，这次毅行活动的行程约为20000m，将20000m用科学记数法表示为m.

查看试题解析
10. 一个数的平方是9，这个数是.

查看试题解析
11. 木工师得要将一根木条固定在墙上，通常需要钉两根钉子，请你写出这一现象反映的一个数学基本事实.

查看试题解析
12. 比较大小；-|-0.4|-（-0.4）.（填“＜”、“=”、“＞”）

查看试题解析
13. 已知x=2是关于x的方程3x=10-ax的解，则a=

查看试题解析
14. 一副三角板如图所示放置，则∠AOB=°.

查看试题解析
15. 如图一个正方体的平面展开图，若将它折叠成正方体，相对的两个面上的数字互为相反数，则xy=.

查看试题解析
16. 如图，直线AB和直线CD相交于点O，OE平分∠BOD，若∠BOE=26°30′.则∠AOC=.

查看试题解析
17. 已知a-3b=2，则（3b-a）²+4（a-3b）-17=.

查看试题解析
18. 小明和小红两人做游戏，小明对小红说：“你任意想一个数，把这个数加上5，然后乘以2接着减去4，最后除以2，把得到的结果告诉我，我就知道你想的是什么数结果小红把按规则计算出结果为20告诉了小明.”如果你是小明，你应该告诉小红，她想的数是.

查看试题解析

三、解答题

19. 计算：

(1)、-15-[-1-（4-2²×5）]

(2)、-1²⁰¹⁹-（1- $\frac{1}{2}$ ）÷|3-（-3）²|

查看试题解析
20. 对于有理数a、b，定义运算：“★”，当a≥b时，a★b=2a-3b，当a＜b时，a★b= $\frac{a}{2} + \frac{b}{3}$ .

(1)、计算：（x+2）★（x+1）的值；

(2)、若（x+1）★（2x-1）=-1，求x的值.

查看试题解析
21. 我县盛产绿色蔬菜，生产销售一种绿色蔬菜，若在市场上直接销售，每吨利润为800元，经粗加工销售，每吨利润可达2000元，经精加工后销售，每吨利润涨至2500元.我县一家农工商公司采购这种蔬菜若干吨生产销售，若单独进行精加工，需要30天才能完成，若单独进行粗加工，需要20天才能完成.已知每天单独粗加工比单独精加工多生产10吨.

(1)、试问这家农工商公司采购这种蔬菜共多少吨？

(2)、由于两种加工方式不能同时进行受季节条件限制，公司必须在24天内将这批蔬菜全部销售或加工完毕，为此该公司研制了三种可行方案：
方案一：将蔬菜全部进行粗加工；

方案二：尽可能多的对蔬菜进行精加工，没有来得及进行加工的蔬菜，在市场上直接销售；

方案三：将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好24天完成，你认为选择哪种方案获利最多？请通过计算说明理由.

查看试题解析
22. 化简或解方程：

(1)、化简：3a²-[5a-（2a-3）+4a²]

(2)、解方程： $\frac{2 x - 1}{3}$ +1= $\frac{2 x + 1}{6}$

查看试题解析
23. 如图，点C在线段AB上，AC：BC=3：2，点M是AB的中点，点N是BC的中点，若AB=10cm，求线段MN的长.

查看试题解析

24. 某水果商店经销一种苹果，共有20筐，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如表：

与标准质量的差值（单位；千克）	-3	-2	-1.5	0	1	2.5
筐数	1	4	2	3	2	8

(1)、这20筐苹果中，最重的一筐比最轻的一筐多重多少千克？

(2)、与标准重量比较，这20筐苹果总计超过或不足多少千克？

(3)、若苹果每千克售价

8.5

元，则出售这20筐苹果可卖多少元？

查看试题解析

25. 已知：A＝2a²＋3ab－2a－1，B＝－a²＋ab－1

(1)、求3A＋6B的值；

(2)、若3A＋6B的值与a的取值无关，求b的值.

查看试题解析
26. 如图，两摞规格完全相同的课本整齐叠放在讲台上请根据图中所给出的数据信息，回答下列问题：

(1)、每本课本的厚度为cm；

(2)、若有一摞上述规格的课本x本，整齐叠放在讲台上，请用含x的代数式表示出这一摞数学课本的顶部距离地面的高度为cm；

(3)、当x=48时，若从中取走10本，求余下的课本的顶部距离地面的高度.

查看试题解析
27. 已知关于m的方程 $\frac{1}{2}$ （m-16）=7的解也是关于x的方程2（x-3）-n=52的解.

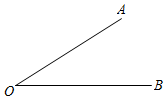(1)、求m，n的值；

(2)、已知∠AOB=m°，在平面内画一条射线OP，恰好使得∠AOP=n∠BOP，求∠BOP.

查看试题解析

28. 随着出行方式的多样化，某地区打车有三种乘车方式，收费标准如下（假设打车的平均车速为30千米/小时）：

网约出租车	网约顺风车	网约专车
3千米以内：12元	1.5元/千米	2元/千米
超过3千米的部分：2.4元/千米	0.5元/分钟	0.6元/分钟

（如：乘坐6千米，耗时12分钟，网约出租车的收费为：12+2.4×（6-3）=19.2（元）；网约顺风车的收费为：6×1.5+12×0.5=15（元）；网约专车的收费为：6×2+12×0.6=19.2（元））

请据此信息解决如下问题：

(1)、王老师乘车从纵棹园去汽车站，全程8千米，如果王老师乘坐网约出租车，需要支付的打车费用为元；

(2)、李校长乘车从纵掉园去生态园，乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程；

(3)、网约专车为了和网约顺风车竞争客户，分别推出了优惠方式：网约顺风车对于乘车路程在5千米以上（含5千米）的客户每次收费立减6元；网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.

查看试题解析

记录周次	第一周	第二周	第三周	第四周
平均气温	3℃	0℃	-5℃	-2℃