江苏省扬中市六校联考2018-2019学年七年级上学期数学期末考试试卷

试卷更新日期：2020-01-08 类型：期末考试

进入出卷网下载

一、单选题

1. |﹣2019|等于（）

A、2019 B、﹣2019 C、 $\frac{1}{2019}$ D、﹣ $\frac{1}{2019}$

查看试题解析
2. 2018年泰兴国际半程马拉松全程约为21097.5米，将21097.5用科学记数法表示为（）

A、 21.0975×10³ B、2.10975×10⁴ C、21.0975×10⁴ D、2.10975×10⁵

查看试题解析
3. 若 $x = 5$ 是关于x的方程 $2 x + 3 m - 1 = 0$ 的解，则m的值为（）

A、 $- 3$ B、 $- 2$ C、 $- 1$ D、0

查看试题解析
4. 如图，数轴上点P表示的数可能是（）

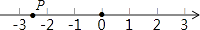A、﹣2.66 B、﹣3.57 C、﹣3.2 D、﹣1.89

查看试题解析
5. 下列各组单项式中，是同类项的一组是（）

A、3x³y与3xy³ B、2ab²与-3a²b C、a²与b² D、2xy与3 yx

查看试题解析
6. 如图，正方形硬纸片ABCD的边长是8，点E、F分别是AB、BC的中点，若沿图中的虚线剪开，拼成如图的一座“小房子”，则图中阴影部分的面积是（）

A、4 B、8 C、16 D、32

查看试题解析

二、填空题

7. 比较大小：-3-0.1.

查看试题解析
8. 单项式 $- \frac{1}{2} x^{2} y$ 的次数是.

查看试题解析
9. 已知∠α=34°，则∠α的补角为°．

查看试题解析
10. 代数式x²-2x=2，则代数式3x²-6x-1的值为.

查看试题解析
11. 在体育课上某同学立定跳远的情况如图所示，l表示起跳线，在测量该同学的实际立定跳远成绩时，应测量图中线段PC的长，理由是.

查看试题解析
12. 如图是正方体的表面展开图，则与“建”字相对的字是.

查看试题解析
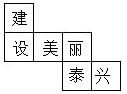13. 如图，直线AB、CD相交于点D，∠BOD与∠BOE互为余角，∠AOC=72°，则∠BOE=°.

查看试题解析
14. 某商店因换季将某种服装打折销售，如果每件服装按标价的5折出售将亏20元，而按标价的8折出售将赚40元，设每件服装的标价是x元，则可列方程为.

查看试题解析
15. 一组“数值转换机”按下面的程序计算，如果输入的数是10，那么输出的结果为19，要使输出的结果为13，则输入的最小正整数是.

查看试题解析
16. 如图，已知线段AB长度为16，线段CD长度为3，线段CD在线段AB上自由运动（点C与A点不重合，D与B点不重合），若点E为AC的中点.则2BE-BD的值为.

查看试题解析

三、解答题

17. 计算：

(1)、 $6 - (- \frac{3}{4}) + (- 5) - \frac{3}{4}$

(2)、 ${(- 1)}^{4} - [(- 3) \times (- \frac{1}{3}) + (- 6) \div \frac{1}{2}]$

查看试题解析
18. 先化简，再求值：已知x²-（2x²-4y）+2（x²-y），其中x=-2，y= $\frac{1}{2}$ .

查看试题解析
19. 如图，C为线段AD上一点，点B为线段CD的中点，且AD=8cm，BD=2cm.

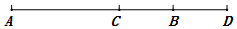(1)、图中共有条线段；

(2)、若点E在线段AD上，且EA=3cm，求线段AC和BE的长.

查看试题解析
20. 如图， $∠ AOD = 150^{\circ}$ ， $∠ AOB = 20^{\circ}$ ， $∠ COD = 40^{\circ}$ ，把 $∠ AOB$ 绕O点以每秒 $5^{\circ}$ 的速度顺时针方向旋转，同时 $∠ COD$ 绕O点以每秒 $4^{\circ}$ 的速度逆时针方向旋转 $.$ 设旋转后的两个角分别记为 $∠ A_{1} {OB}_{1}$ 、 $∠ C_{1} {OD}_{1}$ ，旋转时间为t秒 $(0 \leq t \leq 26)$ .

(1)、当 $t = 1$ 秒时， $∠ B_{1} {OC}_{1} =$ $^{\circ}$ ；

(2)、若射线 ${OB}_{1}$ 与 ${OC}_{1}$ 重合时，求t的值；

(3)、若射线 ${OB}_{1}$ 恰好平分 $∠ C_{1} {OD}_{1}$ 时，求t的值；

(4)、在整个旋转过程中，有秒 $∠ B_{1} {OC}_{1}$ 小于或等于 $10^{\circ}$ ？ $($ 直接写出结论 $)$

查看试题解析
21. 解方程：

(1)、 $2 (x - 1) + 3 = 0$ ；

(2)、 $\frac{x - 1}{2} = \frac{1}{3} + x$ .

查看试题解析
22. 根据如图所示的主视图、左视图、俯视图，想象这个物体的形状，解决下列问题：

(1)、说出这个几何体的名称；

(2)、若如图所示的主视图的长、宽分别为5、2，求该几何体的体积.（结果保留π）

查看试题解析
23. 画图题：

(1)、在如图所示的方格纸中，经过线段AB外一点C，不用量角器与三角尺，仅用直尺画线段AB的垂线CD和平行线CE（其中D、E为格点）.

(2)、连接AC和BC，若图中每个最小正方形的边长为1，试求三角形ABC的面积是.

查看试题解析
24. 用一元一次方程解决问题：
运动场环形跑道周长400米，小红跑步的速度是爷爷的 $\frac{5}{3}$ 倍，他们从同一起点沿跑道的同一方向同时出发，5分钟后小红第一次与爷爷相遇.小红和爷爷跑步的速度各多少？
分析：设爷爷跑步的速度是xm/min，可以列出表格：

速度/（m/min）
时间/min
路程/m
爷爷
x
5
5x
小红
______
5
______
也可画出如下的线形示意图：

(1)、请将上面表格、线形示意图中的空白处补充完整；

(2)、根据上面的分析，列出方程并解决问题.
解：设爷爷跑步的速度是xm/min，根据题意得：.

查看试题解析
25. 用“⊗”规定一种新运算：对于任意有理数a和b，规定a⊗b=ab²+2ab+a.如：1⊗3=1×3²+2×1×3+1=16

(1)、求2⊗（-1）的值；

(2)、若（a+1）⊗3=32，求a的值；

(3)、若m=2⊗x，n=（ $\frac{1}{4}$ x）⊗3（其中x为有理数），试比较m、n的大小.

查看试题解析

26. 观察下表三组数中每组数的规律后，回答下列问题：

序号	1	2	3	4	5	6	7	…	n
A组	3	5	7	9	11	13	15	…	______
B组	5	8	13	20	29	40	______	…	n²+4
C组	4	8	16	32	64	128	256	…	______

(1)、请完成上表中三处空格的数据；

(2)、可以预见，随着n值的逐渐变大，三组数中，值最先超过10000的是组；

(3)、在A组的数中任意圈出连续的三个数，例如圈出5、7、9求它们的和为21.问能否圈出这样的三个数，使它们的和为607？若能，请求出这三个数；若不能，请说明理由；

(4)、下面再给出D组数，观察它与C组的关系，写出D组的第n个数：.

D组1，11，13，35，61，131，253，…

（提示：将D组每个数分别减去C组中对应位置的数，看看发现什么？）

查看试题解析

	速度/（m/min）	时间/min	路程/m
爷爷	x	5	5x
小红	______	5	______